Question

8．设F₁、F₂分别是椭圆的左、右焦点，若在直线x=$\frac{{a}^{2}}{c}$上存在点P，使线段PF₁的中垂线过点F₂，则椭圆的离心率的取值范围是[$\frac{\sqrt{3}}{3}，1$）．

Answer 1

分析 设x=$\frac{{a}^{2}}{c}$与x轴的交点为Q，连结PF₂，根据平面几何的知识可得|PF₂|=|F₁F₂|=2c，且|PF₂|≥|QF₂|，由此得到关于a、c的不等关系，化简得到关于离心率e的一元二次不等式，求解一元二次不等式后与椭圆离心率的范围取交集得答案．

解答 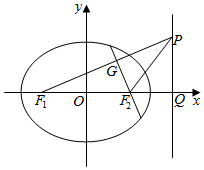解：如图，
设x=$\frac{{a}^{2}}{c}$与x轴的交点为Q，连结PF₂，
∵PF₁的中垂线过点F₂，
∴|F₁F₂|=|PF₂|，可得|PF₂|=2c，
∵|QF₂|=$\frac{{a}^{2}}{c}-c$，且|PF₂|≥|QF₂|，
∴2c≥$\frac{{a}^{2}}{c}$-c，两边都除以a得，
2•$\frac{c}{a}$≥$\frac{a}{c}-\frac{c}{a}$，
即2e≥$\frac{1}{e}-e$，整理得3e²≥1，
解得e≥$\frac{\sqrt{3}}{3}$，又e∈（0，1），
∴椭圆的离心率的取值范围是[$\frac{\sqrt{3}}{3}，1$）．
故答案为：[$\frac{\sqrt{3}}{3}，1$）．

点评 本题考查椭圆的简单性质，考查了椭圆离心率的范围的求法，着重考查平面几何知识在解圆锥曲线问题中的应用，属于中档题．