
分析 (1)f(x)=ax2-(a+2)x+2=(ax-2)(x-1),a<0,可得ax2-(a+2)x+2=0的两根为$\frac{2}{a}$,且$\frac{2}{a}$<1,即可得出.
(2)f(x)+2x<0化为:g(x)=ax2-ax+2<0,由“$\frac{1}{2}$≤x≤$\frac{3}{4}$”是“f(x)+2x<0”的充分条件,可得$\left\{\begin{array}{l}{g(\frac{1}{2})<0}\\{g(\frac{3}{4})<0}\end{array}\right.$,又a>0,解得a范围.
解答 解:(1)f(x)=ax2-(a+2)x+2=(ax-2)(x-1),∵a<0,∴ax2-(a+2)x+2=0的两根为$\frac{2}{a}$,且$\frac{2}{a}$<1.
∴关于x的不等式f(x)>0的解集为$(\frac{2}{a},1)$.
(2)f(x)+2x<0化为:g(x)=ax2-ax+2<0,
∵“$\frac{1}{2}$≤x≤$\frac{3}{4}$”是“f(x)+2x<0”的充分条件,
∴$\left\{\begin{array}{l}{g(\frac{1}{2})<0}\\{g(\frac{3}{4})<0}\end{array}\right.$,又a>0,解得a>$\frac{32}{3}$.
∴正实数a的取值范围是$(\frac{32}{3},+∞)$.
点评 本题考查了一元二次不等式与一元二次方程的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | -7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-1 | B. | y=1 | C. | y=-2 | D. | y=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,则b∥α | B. | 若a⊥α,b∥α,则a⊥b | ||
| C. | 若a∥b,b?α,则a∥α | D. | 若a,b?α,a∥β,b∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
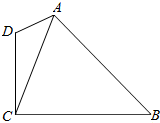 如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com