
分析 根据回归系数的几何意义可判断①;
求出直线与圆的直角坐标系方程,可判断直线与圆的位置关系,可判断②;
根据反比例函数的图象和性质,可判断③;
根据切线方程,求出f(1),f'(1)的值,可判断④.
解答 解:①若回归直线方程$\widehat{y}$=0.2x+12,则 x每增加一个单位时,$\widehat{y}$平均增加0.2个单位;故错误;
②圆ρ=cosθ与直线ρcosθ=1的直角坐标系方程分别为:
(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$;x=1,
圆心($\frac{1}{2}$,0)到直线x=1的距离d=$\frac{1}{2}$=r,
故直线与圆相切,故正确
③函数y=$\frac{1}{x}$在(-∞,0)∪(0,+∞)内为减函数,但在定义域内不具单调性,故错误;
④若y=f(x)在点(1,f(1))处的切线方程是y=$\frac{1}{2}$x+2,
则f(1)=$\frac{5}{2}$,f'(1)=$\frac{1}{2}$.
则f(1)+f'(1)=3.故正确;
故答案为:②④.
点评 本题以命题的真假判断与应用为载体,考查了回归系数的几何意义,极坐标方程,函数的单调性,切线方程,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
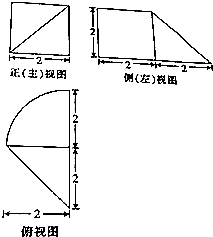
| A. | 2π+$\frac{4}{3}$ | B. | 4π+$\frac{4}{3}$ | C. | 4π+4 | D. | 2π+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A?B | C. | B?A | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com