
| A. | -15 | B. | 15 | C. | 20 | D. | -20 |
分析 由条件求得n=6,再利用二项展开式的通项公式,求得${({\sqrt{x}-\frac{1}{{\sqrt{x}}}})^n}$的展开式中的常数项.
解答 解:∵(1+x)+(1+x)2+(1+x)3+…+(1+x)n=a0+a1x+a2x2+…+anxn,
∴令x=1,可得2+22+23+…+2n=a0+a1+a2+…+an=126,即 $\frac{2(1{-2}^{n})}{1-2}$=126,2n+1=128,∴n=6.
根据 ${({\sqrt{x}-\frac{1}{{\sqrt{x}}}})^n}$=${(\sqrt{x}-\frac{1}{\sqrt{x}})}^{6}$ 的通项公式为Tr+1=${C}_{6}^{r}$•(-1)r•x3-r,
令3-r=0,求得r=3,可得展开式中的常数项为-${C}_{6}^{3}$=-20,
故选:D.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
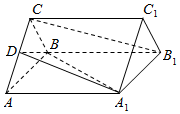 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线y=-$\frac{1}{2}$x | B. | 直线y=$\frac{1}{2}$x | C. | 直线y=-$\frac{1}{2}$ | D. | 直线x=-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
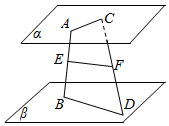 已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β
已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com