
分析 由题意可得$\sqrt{{a}^{2}+{b}^{2}}$=2,既有a2+b2=4,①,又f($\frac{π}{6}$)=$\frac{a}{2}$+$\frac{\sqrt{3}b}{2}$=$\sqrt{3}$代入①,结合ab≠0,即可解得a,b的值,从而可求f($\frac{π}{3}$)的值.
解答 解:f(x)=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+θ),
所以f(x)max=$\sqrt{{a}^{2}+{b}^{2}}$=2,
所以a2+b2=4,①
f($\frac{π}{6}$)=$\frac{a}{2}$+$\frac{\sqrt{3}b}{2}$=$\sqrt{3}$,②
则有:ab≠0,
将②代入①,化简得:(b-1)(b-2)=0,
解得,b=1,a=$\sqrt{3}$或,b=2,a=0(不满足ab≠0,舍去)
所以:f($\frac{π}{3}$)=$\frac{\sqrt{3}a}{2}$+$\frac{b}{2}$=$\frac{3}{2}+\frac{1}{2}$=2.
点评 本题主要考查了两角和与差的正弦函数公式,正弦函数的图象和性质,属于基本知识的考查.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
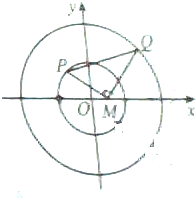 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.
如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com