
【题目】已知函数![]()
![]() .
.
(Ⅰ)若![]() 在区间
在区间![]() 上有极值,求实数
上有极值,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 有唯一的零点
有唯一的零点![]() ,试求
,试求![]() 的值.(注:
的值.(注:![]() 为取整函数,表示不超过
为取整函数,表示不超过![]() 的最大整数,如
的最大整数,如![]() ;以下数据供参考:
;以下数据供参考:![]() )
)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)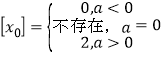 .
.
【解析】
试题分析:(1)求出f(x)的导数,令h(x)=2x3﹣ax﹣2,x∈(0,+∞),求出导数,讨论a的符号,判断单调性,即可得到所求a的范围;(2)由(1)可知:f(1)=3知x∈(0,1)时,f(x)>0,则x0>1,讨论f(x)在x>1的单调性,再由零点的定义和极值点的定义,可得x0的方程,构造函数![]() ,判断单调性,由零点存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
,判断单调性,由零点存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
试题解析:
(Ⅰ)函数![]()
![]() 的定义域为
的定义域为![]() ,
,
![]()
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上为增函数,
上为增函数,
又![]() 函数
函数![]() 在
在![]() 内有一个零点
内有一个零点![]() ,
,
且当![]() 时,
时,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 内有极小值.
内有极小值.
当![]() 时,
时,![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
![]() 函数
函数![]() 在
在![]() 单调递减,此时函数
单调递减,此时函数![]() 无极值,
无极值,
综上可得:![]() 在区间
在区间![]() 内有极值时实数
内有极值时实数![]() 的取值范围是
的取值范围是![]() ,
,
(Ⅱ)①当![]() 时,
时,![]() 得
得![]() ,不满足定义域,
,不满足定义域,![]() 不存在.
不存在.
②当![]() 时,由(Ⅰ)知:若
时,由(Ⅰ)知:若![]() 有唯一的零点
有唯一的零点![]() 为极小值点,
为极小值点,
所以![]() ,
,
③当![]() 时,函数
时,函数![]() 的定义域为
的定义域为![]() ,
,
由(Ⅰ)可知:![]() 知
知![]() 时,
时,![]()
又![]() 在区间
在区间![]() 上只有一个极小值点记为
上只有一个极小值点记为![]() ,
,
且![]() 时,
时,![]() 函数
函数![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
由题意可知:![]() 即为
即为![]() ,
,
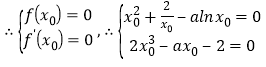 消去可得:
消去可得:![]() ,
,
即![]() ,
,
令![]() ,则
,则![]() 在区间
在区间![]() 上单调递增,
上单调递增,
又![]() ,
,
![]() ,
,
由零点存在性定理知![]()
![]()
综上可得: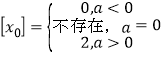


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线![]() 的左,右焦点分别为F1,F2,过F1的直线l交双曲线左支于A,B两点,则|BF2|+|AF2|的最小值为( )
的左,右焦点分别为F1,F2,过F1的直线l交双曲线左支于A,B两点,则|BF2|+|AF2|的最小值为( )
A. ![]() B. 11
B. 11
C. 12 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
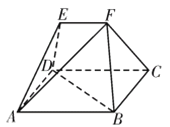
(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:

(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系
之间存在线性相关关系
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量;
(2)公司在2017年年终总结时准备从该年8~12月份这5个月中抽取3个月的数据进行重点分析,求没有抽到9月份数据的概率.
参考数据: ![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 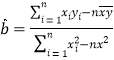 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com