
分析 (1)求出函数的导数,得到f′(0)=0,求出b的值即可;
(2)求出f(x)的导数,通过讨论a的范围,求出导函数的单调性,从而判断出f(x)的单调性,从而求出a的范围即可;
(3)问题等价于$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$,结合(2),取$x=\frac{1}{n}$,得:对于任意正整数n都有$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$成立;令n=1000得证.
解答 解:(1)因为y=f(x)与x轴相切于坐标原点,
故f'(0)=0,故b=1,
(2)$f'(x)=-aln(1+x)+\frac{1-ax}{1+x}-1$,x∈[0,1],
$f''(x)=-\frac{ax+2a+1}{{{{(1+x)}^2}}}$.
①当$a≤-\frac{1}{2}$时,由于x∈[0,1],
有$f''(x)=-\frac{ax+2a+1}{{{{(1+x)}^2}}}≥0$,
于是f'(x)在x∈[0,1]上单调递增,
从而f'(x)≥f'(0),
因此f(x)在x∈[0,1]上单调递增,
即f(x)≥f(0)=0,而且仅有f(0)=0,符合;
②当a≥0时,由于x∈[0,1],
有$f''(x)=-\frac{ax+2a+1}{{{{(1+x)}^2}}}<0$,
于是f'(x)在x∈[0,1]上单调递减,
从而f'(x)≤f'(0)=0,
因此f(x)在x∈[0,1]上单调递减,
即f(x)≤f(0)=0不符;
③当$-\frac{1}{2}<a<0$时,令$m=min\left\{{1,-\frac{2a+1}{a}}\right\}$,
当x∈[0,m]时,$f''(x)=-\frac{ax+2a+1}{{{{({1+x})}^2}}}<0$,
于是f'(x)在x∈[0,m]上单调递减,
从而f'(x)≤f'(0)=0,
因此f(x)在x∈[0,m]上单调递减,
即f(x)≤f(0)=0,而且仅有f(0)=0,不符.
综上可知,所求实数a的取值范围是$(-∞,-\frac{1}{2}]$.
(3)对要证明的不等式等价变形如下:
对于任意的正整数n,不等式${(1+\frac{1}{n})^{n+\frac{2}{5}}}<e$恒成立,
等价变形$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$,
相当于(2)中$a=-\frac{2}{5}$,$m=\frac{1}{2}$的情形,
f(x)在$x∈[{0,\frac{1}{2}}]$上单调递减,
即f(x)≤f(0)=0,而且仅有f(0)=0;
取$x=\frac{1}{n}$,得:对于任意正整数n都有$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$成立;
令n=1000得证.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
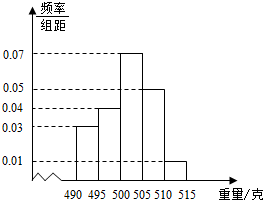 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
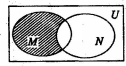 设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )
设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )| A. | {x|2≤x≤3} | B. | {x|1≤x≤2} | C. | $\{x|1≤x≤\sqrt{3}\}$ | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| K2>K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com