练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若不等式|ax＋2|<4的解集为(－1,3)，则实数a等于(　　)

    A．8　　　　                                                 B．2　　　　

    C．－4　　 　                                               D．－2


    　D

    [解析]　由－4<ax＋2<4，得－6<ax<2.

    ∴(ax－2)(ax＋6)<0，其解集为(－1,3)，∴a＝－2.

    [点评]　可用方程的根与不等式解集的关系求解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设数列{an}的前n项和为Sn，对一切n∈N*，点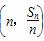都在函数f(x)＝x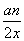＋的图象上．

    (1)求a1、a2、a3的值，猜想an的表达式，并用数学归纳法证明；

    (2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1)，(a2，a3)，(a4，a5，a6)，(a7，a8，a9，a10)；(a11)，(a12，a13)，(a14，a15，a16)，(a17，a18，a19，a20)；(a21)，…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{bn}，求b5＋b100的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，过点(2，)且与极轴平行的直线的方程是(　　)

    A．ρcosθ＝                                             B．ρsinθ＝

    C．ρ＝cosθ                                             D．ρ＝sinθ

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l是过点P(－1,2)，方向向量为n＝(－1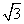，)的直线，圆方程ρ＝2cos(θ＋)．

    (1)求直线l的参数方程；

    (2)设直线l与圆相交于M，N两点，求|PM|·|PN|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，设曲线C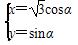：(α为参数)，直线l：ρ(cosθ＋sinθ)＝4.

    (1)写出曲线C的普通方程和直线l的直角坐标方程；

    (2)求曲线C上的点到直线l的最大距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a，b∈R，|a－b|>2，则关于实数x的不等式|x－a|＋|x－b|>2的解集是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式|2x＋1|＋|x－1|<2的解集为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a，b是两个实数，给出下列条件：

    (1)a＋b>1；(2)a＋b＝2；(3)a＋b>2；(4)a2＋b2>2；(5)ab>1.其中能推出“a，b中至少有一个大于1”的条件是(　　)

    A．(2)(3)                                                      B．(1)(2)(3)

    C．(3)                                                           D．(3)(4)(5)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    完成下列程序，输入x的值，求函数y＝|8－2x2|的值．

    ①________，②________.

    查看答案和解析>>

    同步练习册答案