
 如图,平面PBA⊥平面ABCD,∠DAB=90°,PB=AB,BF⊥PA,点E在线段AD上移动.
如图,平面PBA⊥平面ABCD,∠DAB=90°,PB=AB,BF⊥PA,点E在线段AD上移动.分析 (Ⅰ)由已知可证F是PA的中点,连接EF,由中位线的性质可得EF∥PD,又EF?平面PBD,PD?平面PBD,由判定定理即可证明EF∥平面PBD.
(Ⅱ)只要证明DA⊥BF,BF⊥PA,从而证明BF⊥面PDA,又PE?平面PDA,所以无论点E在线段AD的何处,总有PE⊥BF.
解答 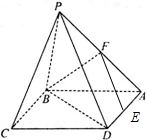 证明:(Ⅰ)因为在三角形PBA中,PB=AB,BF⊥PA,
证明:(Ⅰ)因为在三角形PBA中,PB=AB,BF⊥PA,
所以F是PA的中点,连接EF,…(2分)
在△PDA中,点E,F分别是边AD,PA的中点,
所以EF∥PD…(4分)
又EF?平面PBD,PD?平面PBD
所以EF∥平面PBD.…(6分)
(Ⅱ)因为平面PBA⊥平面ABCD,平面PBA∩平面ABCD=AB,∠DAB=90°,DA⊥AB,DA?平面ABCD
所以DA⊥平面PBA…(8分)
又BF?平面PBA,所以DA⊥BF,又BF⊥PA,PA∩DA=A,PA,DA?平面PDA,
所以BF⊥面PDA…(10分)
又PE?平面PDA所以BF⊥PE
所以无论点E在线段AD的何处,总有PE⊥BF.…(12分)
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的性质,考查了空间想象能力和转化思想,属于基本知识的考查.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
 若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则图中的阴影部分的面积为$\frac{2-\sqrt{3}}{2}$.
若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则图中的阴影部分的面积为$\frac{2-\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了考查某厂2000名工人的生产技能情况,随机抽查了该厂n名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35]),其中产量在[20,25)的工人有6名.
为了考查某厂2000名工人的生产技能情况,随机抽查了该厂n名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35]),其中产量在[20,25)的工人有6名.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com