
【题目】给出下列命题:
(1)存在实数![]() 使
使![]() ;
;
(2)直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
(3)![]() (
(![]() )的值域是
)的值域是![]() ;
;
(4)若![]() ,
,![]() 都是第一象限角,且
都是第一象限角,且![]() ,则
,则![]() .
.
其中正确命题的序号为( )
A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)
【答案】B
【解析】
(1)利用辅助角公式将![]() 可判断(1);
可判断(1);
(2)根据函数y=sinx图象的对称轴方程可判断(2);
(3)根据余弦函数的性质可求出y=cos(cosx)(x∈R)的最大值与最小值,从而可判断(3)的正误;
(4)用特值法令α,β都是第一象限角,且α>β,可判断(4).
解:(1)∵![]() ,∴(1)错误;
,∴(1)错误;
(2)∵y=sinx图象的对称轴方程为![]() ,k=﹣1,
,k=﹣1,![]() ,∴(2)正确;
,∴(2)正确;
(3)根据余弦函数的性质可得cosx![]() , y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
, y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
(4)不妨令![]() ,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
故选:B.


科目:高中数学 来源: 题型:
【题目】某校为提高学生的身体素质,实施“每天一节体育课”,并定期对学生进行体能测验在一次体能测验中,某班甲、乙、丙三位同学的成绩(单位:分)及班内排名如表(假定成绩均为整数)现从该班测验成绩为94和95的同学中随机抽取两位,这两位同学成绩相同的概率是( )
成绩/分 | 班内排名 | |
甲 | 95 | 9 |
乙 | 94 | 11 |
丙 | 93 | 14 |
A.0.2B.0.4C.0.5D.0.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为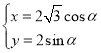 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的值;
的值;
(2)若矩形![]() 内接于曲线
内接于曲线![]() 且四边与坐标轴平行,求其周长的最大值.
且四边与坐标轴平行,求其周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() 为坐标原点.
为坐标原点.
(1)证明:点![]() 在
在![]() 轴的右侧;
轴的右侧;
(2)设线段![]() 的垂直平分线与
的垂直平分线与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() .若
.若![]() 与
与![]() 的面积相等,求直线
的面积相等,求直线![]() 的斜率
的斜率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,…,
,…,![]() 为1,2,…,10的一个排列,则满足对任意正整数m,n,且
为1,2,…,10的一个排列,则满足对任意正整数m,n,且![]() ,都有
,都有![]() 成立的不同排列的个数为( )
成立的不同排列的个数为( )
A.512B.256C.255D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 C 经过点 (2,3),它的渐近线方程为 y = ±![]() .椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
.椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
(1)求双曲线 C 和椭圆 C1 的方程;
(2)经过椭圆 C1 左焦点 F 的直线 l 与椭圆 C1 交于 A、B 两点,是否存在定点 D ,使得无论 AB 怎样运动,都有∠ADF = ∠BDF ?若存在,求出 D 点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com