
分析 (1)Sn=Tn-Tn-1,从而Sn-1=2Sn-2+(n-1).故Sn-Sn-1=2(Sn-1-Sn-2)+1,即an=2an-1+1.显然有an+1=2(an-1+1);
(2)利用错位相减法,放缩法即可比较.
解答 证明:(1)∵2Tn=4Sn-(n2+n),
∴2T1=4S1-(12+1),
即a1=1.
Sn=Tn-Tn-1
=2Sn-$\frac{{n}^{2}+n}{2}$-2Sn-1+$\frac{(n-1)^{2}+(n-1)}{2}$
整理,得Sn=2Sn+n,
从而Sn-1=2Sn-2+(n-1).
故Sn-Sn-1=2(Sn-1-Sn-2)+1,
即an=2an-1+1.
显然有an+1=2(an-1+1).
所以数列{an+1}是以2为首项,2为公比的等比数列;
(2)由(Ⅰ)知bn=$\frac{n+1}{{2}^{n}}$,
则Sn=1+$\frac{3}{{2}^{2}}$+$\frac{4}{{2}^{3}}$+$\frac{5}{{2}^{4}}$+…+$\frac{n+1}{{2}^{n}}$,①,
$\frac{1}{2}$Sn=$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{4}{{2}^{4}}$+…+$\frac{n}{{2}^{n}}$+$\frac{n+1}{{2}^{n+1}}$,②,
则①-②得$\frac{1}{2}$Sn=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n+1}{{2}^{n+1}}$=1+$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-$\frac{n+1}{{2}^{n+1}}$<1+$\frac{1}{2}$,
故Sn<3,
所以b1+b2+…+bn<3
点评 本题是数列与函数、不等式相结合的综合题,主要考查错位相减法和放缩法,考查了分析问题与解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
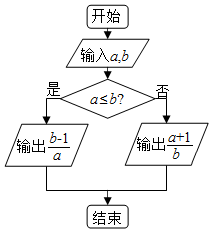 若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )
若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )| A. | $\frac{13}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
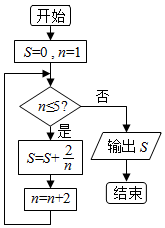
| A. | $\frac{8}{3}$ | B. | $\frac{46}{15}$ | C. | $\frac{25}{6}$ | D. | $\frac{137}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
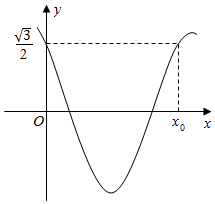 已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com