练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．某几何体的三视图如图所示，则该几何体的体积为（　　）
    A．$\frac{8}{3}$B．$\frac{11}{3}$C．4D．$\frac{14}{3}$

    分析 由三视图可得，直观图为三棱锥和三棱柱的组合体，底面为俯视图中的三角形，高为2，即可求出体积．

    解答 解：由三视图可得，直观图为三棱锥和三棱柱的组合体，
    底面为俯视图中的三角形，高为2，
    体积为$\frac{1}{2}×1×2×2$+$\frac{1}{3}×$$\frac{1}{2}×1×2×2$=$\frac{8}{3}$，
    故选A．

    点评 本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．下列说法错误的是（　　）
    A．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
    B．在线性回归分析中，回归直线不一定过样本点的中心（$\overline{x}$，$\overline{y}$）
    C．在回归分析中，R2为0.98的模型比R2为0.80的模型拟合的效果好
    D．自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知平面向量$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），那么$\overrightarrow{a}$•$\overrightarrow{b}$=x1x2+y1y2；空间向量$\overrightarrow{a}$=（x1，y1，z1），$\overrightarrow{b}$=（x2，y2．z2），那么$\overrightarrow{a}$•$\overrightarrow{b}$=x1x2+y1y2+z1z2．由此推广到n维向量：$\overrightarrow{a}$=（a1，a2，…，an），$\overrightarrow{b}$=（b1，b2，…，bn），那么$\overrightarrow{a}$•$\overrightarrow{b}$=a1b1+a2b2+a3b3+…+anbn．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．（1-x）5（1+$\sqrt{x}$）2的展开式中x4的系数为（　　）
    A．-10B．-5C．10D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

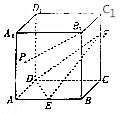    9．如图，在正方体ABCD-A1B1C1D1中，E是AB的中点，F在CC1上，且CF=2FC1，点P是侧面AA1D1D（包括边界）上一动点，且PB1∥平面DEF，则tan∠ABP的取值范围是（　　）
    A．[$\frac{1}{2}$，$\frac{3}{2}$]B．[0，1]C．[$\frac{1}{3}$，$\frac{\sqrt{10}}{3}$]D．[$\frac{1}{3}$，$\frac{\sqrt{13}}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

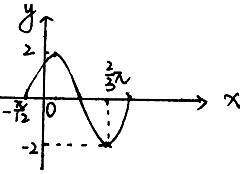    19．若函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$），如图所示
    （1）求f（x）的解析式
    （2）若方程f（x）=m在x∈[0，$\frac{π}{2}$]有且只有一个实根，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

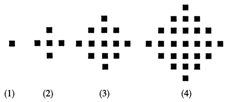    6．某少数民族的刺绣有着悠久的历史，如图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
    （1）由图归纳出f（n）与f（n-1）的关系式，并求出f（n）表达式；
    （2）求证：$\frac{1}{f（1）}$+$\frac{1}{f（2）-1}$+$\frac{1}{f（3）-1}$+…+$\frac{1}{f（n）-1}$$＜\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数$f（x）=sin（2x+\frac{π}{6}）+sin（2x-\frac{π}{6}）+cos2x+1$
    （1）求函数f（x）的对称中心和函数的单调递增区间；
    （2）已知△ABC中，角A，B，C的对边分别为a，b，c，若$f（A）=3，B=\frac{π}{4}，a=\sqrt{3}$，求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知{an}为等差数列，Sn为数列{an}的前n项和，平面内三个不共线向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，满足$\overrightarrow{OC}=（{{a_{17}}-3}）\overrightarrow{OA}+{a_{2001}}\overrightarrow{OB}$，若点A，B，C在一条直线上，则S2017=（　　）
    A．2017B．4034C．2016D．4032

    查看答案和解析>>

    同步练习册答案