
| A. | [$\frac{4}{3},3$] | B. | [$\frac{4}{3},2$] | C. | [$\frac{4}{3},2$) | D. | [$\frac{4}{3},+∞$) |
分析 由对数函数和二次函数的性质易得函数的单调递增区间,只需让(3m-2,m+2)是其子区间即可,由此可得m的不等式组,解不等式组可得.
解答 解:先保证对数有意义-x2+4x+5>0,解得-1<x<5,
又可得二次函数y=-x2+4x+5的对称轴为x=-$\frac{4}{2×(-1)}$=2,
由复合函数单调性可得函数f(x)=log${\;}_{\frac{1}{2}}$(-x2+4x+5)的单调递增区间为(2,5),
要使函数f(x)=log${\;}_{\frac{1}{2}}$(-x2+4x+5)在区间(3m-2,m+2)内单调递增,
只需$\left\{\begin{array}{l}{3m-2≥2}\\{m+2≤5}\\{3m-2<m+2}\end{array}\right.$,解关于m的不等式组得$\frac{4}{3}$≤m<2,
故选:C.
点评 本题考查对数函数的性质,涉及复合函数的单调性和不等式组的解法,属基础题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
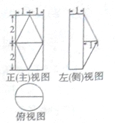
| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2m,-m-4) | B. | (5,1) | C. | (-1,-2) | D. | (2m,m+4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com