
| A. | y=±$\frac{{\sqrt{5}}}{2}$x | B. | y=±$\frac{{2\sqrt{5}}}{5}$x | C. | y=±$\frac{2}{3}$x | D. | y=±$\frac{3}{2}$x |
分析 通过点M(-6,5)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上及双曲线C的焦距为12,可得$\frac{36}{{a}^{2}}-\frac{25}{{b}^{2}}=1$、a2+b2=36,计算即得结论.
解答 解:∵点M(-6,5)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,
∴$\frac{36}{{a}^{2}}-\frac{25}{{b}^{2}}=1$,①
又∵双曲线C的焦距为12,
∴12=2$\sqrt{{a}^{2}+{b}^{2}}$,即a2+b2=36,②
联立①、②,可得a2=16,b2=20,
∴渐近线方程为:y=±$\sqrt{\frac{{b}^{2}}{{a}^{2}}}$x=±$\frac{\sqrt{5}}{2}$x,
故选:A.
点评 本题考查求双曲线的渐近线,注意解题方法的积累,属于基础题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
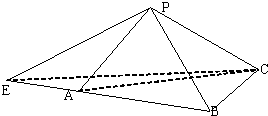 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.
如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ③⑤ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 中间一项的二项式系数最大 | B. | 中间两项的二项式系数相等且最大 | ||
| C. | 中间两项的二项式系数相等且最小 | D. | 中间两项的二项式系数互为相反数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\frac{1}{2}$)-x | B. | y=sinx2 | C. | y=x|x| | D. | y=ln|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com