Question

8．实数x，y满足$\left\{\begin{array}{l}{y≥1}\\{y-2x+1≤0}\\{x+y-8≤0}\end{array}\right.$，则z=x-y的最小值为（　　）

• A． 2
• B． 1
• C． -1
• D． -2

Answer 1

分析 由已知，画出平面区域，将目标函数变形为y=x-z的形式，求z的最小值即求直线在y轴截距的最大值．

解答 解：由已知，不等式组表示的平面区域如图，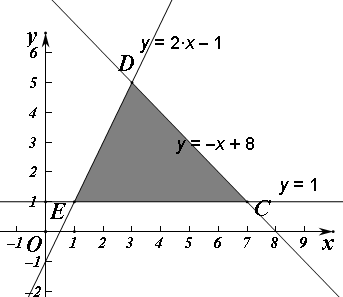
实数x，y满足的平面区域为图中阴影部分，所以当直线为y=x-z经过D时，使得-z最大，即z最小，由$\left\{\begin{array}{l}{y-2x+1=0}\\{x+y-8=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$
得到D的坐标为（3，5），
所以z=x-y的最小值为3-5=-2；
故选D．

点评 本题考查了不等式组表示的平面区域的画法以及目标函数最值的求法；关键是正确画图，找出使目标函数取最值的点．