Question

15．M是抛物线y²=2x上-点，P点坐标为（3，$\frac{10}{3}$），设d是点M到准线的距离，要使d+|MP|最小，则点M的坐标为（2，2）．

Answer 1

分析 先判断出P（3，$\frac{10}{3}$）在抛物线y²=2x的外部，然后做出图形，根据抛物线的定义可得d+|MP|=|PM|+|MF|，故要使d+|MP|取最小值则只有当P，M，F三点共线时成立因此可求出PF所在的直线方程然后与抛物线的方程联立即可求出M点的坐标．

解答 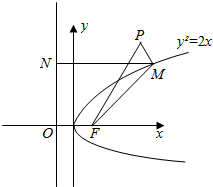解：∵（3，$\sqrt{6}$）在抛物线y²=2x上且$\frac{10}{3}$＞$\sqrt{6}$，
∴P（3，$\frac{10}{3}$）在抛物线y²=2x的外部，
∵抛物线y²=2x的焦点F（$\frac{1}{2}$，0），准线方程为x=-$\frac{1}{2}$，
∴在抛物线y²=2x上任取点M过M作MN⊥直线x=$\frac{1}{2}$，则|MN|=d，
∴根据抛物线的定义可得d=|MF|，
∴d+|MP|=|PM|+|MF|，
∵|PM|+|MF|≥|PF|，
∴当P，M，F三点共线时d+|MP|取最小值，
此时PF所在的直线方程为y-$\frac{10}{3}$=$\frac{4}{3}$（x-3）即4x-3y-2=0，
令$\left\{\begin{array}{l}{4x-3y-2=0}\\{{y}^{2}=2x}\end{array}\right.$，则$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，即当点的坐标为（2，2）时d+|MP|取最小值，
故答案为：（2，2）．

点评 本题主要考察抛物线的性质，属常考题，较难．解题的关键是根据抛物线的定义转化为d+|MP|=|PM|+|MF|．