
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
分析 (1)确定元件A为正品的件数及元件B为正品的件数,由元件A、B各100件,利用古典概型求得结论.
(2)生产5件元件B中正品有n件,则次品有5-n件,根据题意要求的利润不少于280元列出不等式,解不等式求出n的值,利用独立重复试验概型能求出生产5件元件B所获得的利润不少于280元的概率.
解答 解:(1)由题意元件A为正品的概率为:$\frac{40+32+8}{100}$=$\frac{4}{5}$,
元件B为正品的概率为:$\frac{40+29+6}{100}$=$\frac{3}{4}$.
(2)设生产5件元件B中正品有n件,则次品有5-n件,
依题意得100n-20(5-n)≥280,
解得n$≥\frac{19}{6}$,∴n=4或n=5,
设“生产5件元件B所获得的利润不少于280元“为事件A,
则P(A)=${C}_{5}^{4}(\frac{3}{4})^{4}×\frac{1}{4}+(\frac{3}{4})^{5}$=$\frac{81}{128}$.
∴生产5件元件B所获得的利润不少于280元的概率为$\frac{81}{128}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意古典概型和独立重复试验概型的合理运用.


科目:高中数学 来源: 题型:解答题
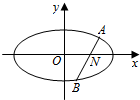 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最小值为1,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最小值为1,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,我海军舰队在亚丁湾执行护航任务中位于点A处南偏西38°的方向且距点A3海里的点B处,点A处一海盗船正挟持人质以10海里/时的速度向北偏西22°方向航行,现护航编队接到求救信号并开始对其进行拦截,假设成功拦截于点C处.
如图,我海军舰队在亚丁湾执行护航任务中位于点A处南偏西38°的方向且距点A3海里的点B处,点A处一海盗船正挟持人质以10海里/时的速度向北偏西22°方向航行,现护航编队接到求救信号并开始对其进行拦截,假设成功拦截于点C处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com