
分析 由函数定义域不同判断①;求出不等式x2>4的解集,结合充分必要条件的判定方法判断②;直接求出函数值判断③;写出命题的逆命题判断④.
解答 解:①$f(x)=\frac{|x|}{x}$的定义域为{x|x≠0},g(x)=$\left\{\begin{array}{l}{1,x≥0}\\{-1,x<0}\end{array}\right.$的定义域为R,定义域不同,不是同一函数,故①错误;
②由x2>4,得x<-2或x>2,∴“x=2”是“x2>4”的既不充分也不必要条件,故②错误;
③若f(x)=|x|-|x-1|,则f($\frac{1}{2}$)=|$\frac{1}{2}$|-|$\frac{1}{2}-1$|=$\frac{1}{2}-\frac{1}{2}=0$,∴$f[f(\frac{1}{2})]$=f(0)=-1,故③错误;
④若x2-2x=0,则x=2的逆命题是若x=2,则x2-2x=0,是真命题,故④正确.
∴正确命题的序号是④.
故答案为:④.
点评 本题考查命题的真假判断与应用,考查函数值的求法,考查了充分必要条件的判定方法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. | 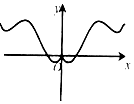 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
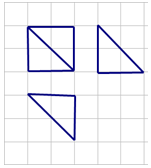
| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}-θ$ | B. | $θ-\frac{π}{2}$ | C. | $\frac{π}{2}+θ$ | D. | θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com