
分析 (1)法一,利用sin2 α+cos2 α=1得出(1-sinα)(1+sinα)=cosα•cosα,从而证明等式成立;
法二,证明$\frac{cosα}{1-sinα}$-$\frac{1+sinα}{cosα}$=0,即可证明等式成立;
(2)利用作差法,证明$\frac{tanαsinα}{tanα-sinα}$-$\frac{tanα+sinα}{tanαsinα}$=0,即可证明等式成立.
解答 解:(1)法一:由sin2 α+cos2 α=1得,
1-sin2 α=cos2 α,即(1-sinα)(1+sinα)=cosα•cosα
∴$\frac{cosα}{1-sinα}$=$\frac{1+sinα}{cosα}$.
法二:$\frac{cosα}{1-sinα}$-$\frac{1+sinα}{cosα}$=$\frac{cosα•cosα-(1+sinα)(1-sinα)}{(1-sinα)cosα}$
=$\frac{{cos}^{2}α-1{+sin}^{2}α}{(1-sinα)cosα}$
=$\frac{1-1}{(1-sinα)cosα}$=0,
∴$\frac{cosα}{1-sinα}$=$\frac{1+sinα}{cosα}$;
(2)∵$\frac{tanαsinα}{tanα-sinα}$-$\frac{tanα+sinα}{tanαsinα}$=$\frac{\frac{sinα}{cosα}•sinα}{\frac{sinα}{cosα}-sinα}$-$\frac{\frac{sinα}{cosα}+sinα}{\frac{sinα}{cosα}•sinα}$
=$\frac{sinα}{1-cosα}$-$\frac{1+cosα}{sinα}$
=$\frac{{sin}^{2}α-(1+cosα)(1-cosα)}{(1-cosα)sinα}$
=$\frac{{sin}^{2}α-1{+cos}^{2}α}{(1-cosα)sinα}$
=$\frac{1-1}{(1-cosα)sinα}$=0,
∴$\frac{tanαsinα}{tanα-sinα}$=$\frac{tanα+sinα}{tanαsinα}$.
点评 本题考查了同角的三角函数基本关系的应用问题,也考查了逻辑推理能力与运算能力的应用问题,是基础题目.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.
如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第6项 | B. | 第7项 | C. | 第11项 | D. | 第6项和第7项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
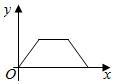 如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )
如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )| A. |  | B. |  | C. | 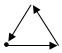 | D. | 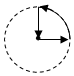 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com