
分析 根据正弦定理可得到$\frac{a}{sinA}=\frac{b}{sinB}$,结合B=2A根据二倍角公式可得$\frac{a}{sinA}=\frac{b}{2sinAcosA}$,整理得到$\frac{b}{a}$=2cosA,再求得A的范围即可得到$\frac{b}{a}$的取值范围.
解答 解:由正弦定理:得$\frac{a}{sinA}=\frac{b}{sinB}$,
∵B=2A,
∴$\frac{a}{sinA}=\frac{b}{2sinAcosA}$,
∴$\frac{b}{a}$=2cosA,
当B为最大角时B<90°,∴A<45°,
当C为最大角时C<90°,∴A>30°,
∴30°<A<45°,
2cos45°<2cosA<2cos30°,
∴$\frac{b}{a}$∈($\sqrt{2}$,$\sqrt{3}$).
故答案为:($\sqrt{2}$,$\sqrt{3}$).
点评 本题主要考查正弦定理和二倍角公式的应用.正弦定理和余弦定理在解三角形中应用比较多,这两个定理和其推论一定要熟练掌握并能够灵活运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
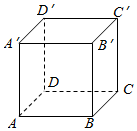 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com