
分析 (Ⅰ)将n换为n+1,两式相减,可得$\frac{{{a_{n+1}}}}{n+1}=\frac{a_n}{n}$=1,进而得到所求通项公式;
(Ⅱ)由n换为n-1,可得${b_n}={2^{n-1}}$,令$f(n)=\frac{S_n}{b_n}=\frac{{{n^2}+n}}{2^n}$,求得f(n+1)-f(n),即可判断f(n)的单调性,进而得到所求最大项.
解答 解:(Ⅰ)由${S_n}=\frac{{({n+1})}}{2}{a_n}$,得${S_{n+1}}=\frac{{({n+2})}}{2}{a_{n+1}}$,
所以${a_{n+1}}={S_{n+1}}-{S_n}=\frac{{({n+2})}}{2}{a_{n+1}}-\frac{{({n+1})}}{2}{a_n}$,
所以$\frac{{{a_{n+1}}}}{n+1}=\frac{a_n}{n}$=1,
故$\left\{{\frac{a_n}{n}}\right\}$是常数列.
所以an=n;
(Ⅱ)一方面,由${a_1}{b_1}+{a_2}{b_2}+…+{a_n}{b_n}=({n-1})•{2^n}+1$知,
当n≥2时$n{b_n}=({n-1})•{2^n}-({n-2})•{2^{n-1}}=n•{2^{n-1}}$,解得${b_n}={2^{n-1}}$,
而a1•b1=1,所以b1=1,适合上式.
故对n∈N*有${b_n}={2^{n-1}}$;
另一方面,令$f(n)=\frac{S_n}{b_n}=\frac{{{n^2}+n}}{2^n}$,
则$f({n+1})-f(n)=\frac{{{{({n+1})}^2}+({n+1})}}{{{2^{n+1}}}}-\frac{{{n^2}+n}}{2^n}=\frac{{-{n^2}+n+2}}{{{2^{n+1}}}}$,
所以f(3)=f(2)>f(1),且f(3)>f(4)>f(5)>…>f(n)>…
故数列$\left\{{\frac{S_n}{b_n}}\right\}$的最大项为f(2)或f(3),即为$\frac{3}{2}$.
点评 本题考查数列的通项公式的求法,注意运用下标变换相减法,考查数列的最大项的求法,注意运用作差法判断数列的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{11}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
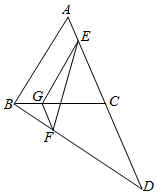 如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.
如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com