
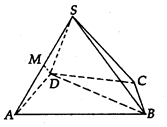
 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.分析 (1)根据线面垂直以及线段的垂直平分线的性质证明即可;
(2)由线线平行到面面平行从而推出线面平行即可.
解答 证明:如图示: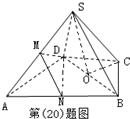
(1)设BD中点为O,连接OC,OE,则由BC=CD知,CO⊥BD,
又已知SC⊥BD,SC⊥CO=C,所以BD⊥平面SOC,
∵△ABD是正三角形,∴AO是BD的中垂线,
故A、O、C在同一直线上,
故平面SAC即平面SOC,
由BD⊥OC,BD⊥SC,得BD⊥平面SAC,
故SA⊥BD;
(2)取AB中点N,连接DM,MN,DN,
∵M是SA的中点,∴MN∥BE,
∵△ABD是正三解形,∴DN⊥AB,
∵∠BCD=120°得∠CBD=30°,∴∠ABC=90°,即BC⊥AB,
所以ND∥BC,所以平面MND∥平面BSC,
故DM∥平面SBC.
点评 本题考查了线面、面面、线线平行的判定定理,考查看图能力,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 数据 | 31,12,22,15,20,45,47,32,34,23,28 |
| A. | 23、32 | B. | 34、35 | C. | 28、32 | D. | 28、35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a不能被2017整除 | B. | b不能被2017整除 | ||
| C. | a、b都不能被2017整除 | D. | a、b中至多有一个能被2017整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B. | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C. | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D. | $\frac{1}{2}$(cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 14种 | C. | 16种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com