
分析 (1)an+1=$\frac{a_n}{{{a_n}+3}}({n∈{N^*}})$,$\frac{1}{{a}_{n+1}}=\frac{{a}_{n}+3}{{a}_{n}}$=1+$\frac{3}{{a}_{n}}$,化简得:$\frac{1}{{a}_{n+1}}+\frac{1}{2}$=3($\frac{1}{{a}_{n}}+\frac{1}{2}$),数列$\left\{{\frac{1}{a_n}+\frac{1}{2}}\right\}$以$\frac{3}{2}$为首项,3为公比的等比数列,
(2){bn}的通项公式${b}_{n}=\frac{2}{{2}^{n-1}}$,前n项和为Tn,Tn=1×$\frac{1}{{2}^{0}}$+2×$\frac{1}{{2}^{1}}$+3×$\frac{1}{{2}^{2}}$+…+(n-1)×$\frac{1}{{2}^{n-2}}$+n×$\frac{1}{{2}^{n-1}}$,采用乘以公比错位相减法,求得Tn=4-$\frac{n+2}{{2}^{n-1}}$,当当n为偶数时,λ<3,当n为奇数时,λ>-2,
综上得:-2<λ<3.
解答 证明:(1)由${a}_{n+1}=\frac{{a}_{n}}{{a}_{n}+3}$<0,得$\frac{1}{{a}_{n+1}}=\frac{{a}_{n}+3}{{a}_{n}}$=1+$\frac{3}{{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}+\frac{1}{2}$=3($\frac{1}{{a}_{n}}+\frac{1}{2}$),$\frac{1}{{a}_{1}}+\frac{1}{2}$=$\frac{3}{2}$,
∴数列$\left\{{\frac{1}{a_n}+\frac{1}{2}}\right\}$以$\frac{3}{2}$为首项,3为公比的等比数列,
$\frac{1}{{a}_{n}}+\frac{1}{2}$=$\frac{3}{2}×$3n-1=$\frac{{3}^{n}}{2}$,
∴${a}_{n}=\frac{2}{{3}^{n}-1}$,
(2)${b}_{n}=\frac{2}{{2}^{n-1}}$,
数列{bn}的前n项和为Tn,Tn=1×$\frac{1}{{2}^{0}}$+2×$\frac{1}{{2}^{1}}$+3×$\frac{1}{{2}^{2}}$+…+(n-1)×$\frac{1}{{2}^{n-2}}$+n×$\frac{1}{{2}^{n-1}}$,
$\frac{1}{2}$Tn=1×$\frac{1}{2}$+2×$\frac{1}{{2}^{2}}$+3×$\frac{1}{{2}^{3}}$+…+(n-1)×$\frac{1}{{2}^{n-1}}$+n×$\frac{1}{{2}^{n}}$,
两式相减:$\frac{1}{2}$Tn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}$,
∴Tn=4-$\frac{n+2}{{2}^{n-1}}$,
(-1)n•λ<4-$\frac{2}{{2}^{n-1}}$,
当n为偶数时,则λ<4-$\frac{2}{{2}^{n-1}}$,λ<3,
当n为奇数时,-λ<4-$\frac{2}{{2}^{n-1}}$,-λ<2,λ>-2,
∴-2<λ<3.
点评 本题考查求等比数列的通项公式,采用乘以公比错位相减法,求前n项和,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$+1 | B. | $\frac{\sqrt{13}+1}{3}$ | C. | $\frac{\sqrt{13}}{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥$\frac{1}{2}$} | B. | {x|x≤-1或x≥$\frac{1}{2}$} | C. | {x|x=-1或x≥$\frac{1}{2}$} | D. | {x|x≤$\frac{1}{2}$或x≥-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
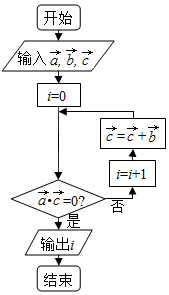 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com