
 ,1+
,1+ +
+ >1,1+
>1,1+ +
+ +…+
+…+
 ,1+
,1+ +
+ +…+
+…+ >2,1+
>2,1+ +
+ +…+
+…+ >
> ,…,由此猜测第n个不等式为________(n∈N+).
,…,由此猜测第n个不等式为________(n∈N+). 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
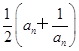 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,f(2)=lg 15,则f(2 008)=________.
,f(2)=lg 15,则f(2 008)=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,把这个结论类比到空间:在三棱锥A-BCD中(如图所示),平面DEC平分二面角A-CD-B且与AB相交于E,则得到的类比的结论是________.
,把这个结论类比到空间:在三棱锥A-BCD中(如图所示),平面DEC平分二面角A-CD-B且与AB相交于E,则得到的类比的结论是________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (x>0),观察f1(x)=f(x)=
(x>0),观察f1(x)=f(x)= ,
,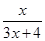 ,
, ,
, ,…
,…查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 n2+
n2+ n,
n, n3+
n3+ n2+
n2+ n,
n, n4+
n4+ n3+
n3+ n2,
n2,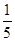 n5+
n5+ n4+
n4+ n3-
n3- n,
n, n5+
n5+ n4+Bn2,…
n4+Bn2,…查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com