
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| ||
1-
|
| 1 |
| 8 |
| 1 |
| 8 |


科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
A、f(0)<f(
| ||
B、f(3)<f(
| ||
C、f(3)<f(0)<f(
| ||
D、f(0)<f(3)<f(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
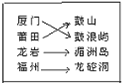 福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).
福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).查看答案和解析>>
科目:高中数学 来源: 题型:
| A、6 | B、7 | C、8 | D、9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n2+n |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2011 |
| 2011 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com