
| A. | (-∞,-$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,+∞) | C. | (-∞,-3] | D. | [-3,+∞) |
分析 依题意,f′(x)=3x2+2ax+b≤0,在[0,1]上恒成立.只需要$\left\{\begin{array}{l}{{f}^{'}(0)=b≤0}\\{{f}^{'}(1)=3+2a+b≤0}\end{array}\right.$即可,由此能求出m=a+b的取值范围.
解答 解:依题意,f′(x)=3x2+2ax+b≤0,在[0,1]上恒成立.
只需要$\left\{\begin{array}{l}{{f}^{'}(0)=b≤0}\\{{f}^{'}(1)=3+2a+b≤0}\end{array}\right.$即可,
∴3+2a+2b≤0,
∴m=a+b≤-$\frac{3}{2}$.
∴m的取值范围是(-∞,-$\frac{3}{2}$].
故选:A.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 132 | B. | 180 | C. | 240 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
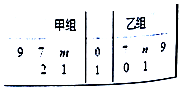 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$或$-\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$或-$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
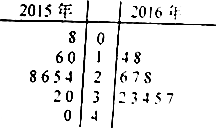 随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )
随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )| A. | $\overline{X}$2015>$\overline{X}$2016,S22015>S22016 | B. | $\overline{X}$2015>$\overline{X}$2016,S22015<S22016 | ||
| C. | $\overline{X}$2015<$\overline{X}$2016,S22015<S22016 | D. | $\overline{X}$2015<$\overline{X}$2016,S22015>S22016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com