
���� ��������������Ϊ$\sqrt{3}$�����߷���Ϊx=$\frac{{\sqrt{3}}}{3}$���г������飬���a��c��b���������˫���ߵķ��̣�
����P��x0��y0����x0y0��0����Բx2+y2=r2�ϣ��õ����߷��̣���˫��������������Τ�ﶨ���������������������⼴�ɣ�
��� �⣺���������⣬��$\left\{{\begin{array}{l}{\frac{a^2}{c}=\frac{{\sqrt{3}}}{3}}\\{\frac{c}{a}=\sqrt{3}}\end{array}}\right.$�����$a=1��c=\sqrt{3}$��
��b2=c2-a2=2��������˫����C�ķ���Ϊ${x^2}-\frac{y^2}{2}=1$����..��4�֣�
����P��x0��y0����x0y0��0����Բx2+y2=r2�ϣ�
Բ�ڵ�P��x0��y0���������߷���Ϊ$y-{y_0}=-\frac{x_0}{y_0}��x-{x_0}��$��
�����$x{x_0}+y{y_0}={r^2}$����..��5�֣�
��$\left\{{\begin{array}{l}{{x^2}-\frac{y^2}{2}=1}\\{x{x_0}+y{y_0}={r^2}}\end{array}}\right.$��ȥy��$��2y_0^2-x_0^2��{x^2}+2{r^2}{x_0}x-{r^4}-2y_0^2=0$��$��2y_0^2-x_0^2��{y^2}-4{r^2}{y_0}y+2{r^4}-2x_0^2=0$�ڡ�..��8�֣�
������ʵ��r ʹ�á�AOBʼ��Ϊ900����$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}=0$��
��${x_1}{x_2}=\frac{{-{r^4}-2y_0^2}}{2y_0^2-x_0^2}$��${y_1}{y_2}=\frac{{2{r^4}-2x_0^2}}{2y_0^2-x_0^2}$��$x_0^2+y_0^2={r^2}$��
x1x2+y1y2=$\frac{{-{r^4}-2y_0^2}}{2y_0^2-x_0^2}+$$\frac{{2{r^4}-2x_0^2}}{2y_0^2-x_0^2}$=$\frac{{{r^4}-2{r^2}}}{2y_0^2-x_0^2}$=0��
$r=\sqrt{2}$��..��10�֣�
��$r=\sqrt{2}$ʱ�ٻ�Ϊ$��3x_0^2-4��{x^2}-4{x_0}x+8-2x_0^2=0$��x0y0��0��
$0��x_0^2��2$��
$��=16x_0^2-4��3x_0^2-4����8-2x_0^2����0$��
������������$r=\sqrt{2}$ʹ�á�AOBʼ��Ϊ90�㡭..��12�֣�
���� ���⿼��˫���߷��̵���ֱ����˫���ߵ�λ�ù�ϵ���ۺ�Ӧ�ã�����������������ⷽ����������������������������ת��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | 3 | C�� | -$\frac{1}{3}$ | D�� | -$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijУ�����ģ�������������11�·ݽ�����һ���������ԣ������ɼ�������±���ʾ����֪�÷ֲ���������ڷ���[400��480���Ŀ����������ȡ27�������������������������Ŀƿ�����ȡ��7������1����a��ֵ��2����ͼ���ĿƲ�����550�ֵ�5�����������ijɼ���������������Ϊ150�֣��ľ�Ҷͼ���������5�����������ijɼ��ķ����3���ڳɼ�������550�ֵ����п����г�ȡ2���������Ʒ����������ٳ鵽һ���������ĸ��ʣ�
ijУ�����ģ�������������11�·ݽ�����һ���������ԣ������ɼ�������±���ʾ����֪�÷ֲ���������ڷ���[400��480���Ŀ����������ȡ27�������������������������Ŀƿ�����ȡ��7������1����a��ֵ��2����ͼ���ĿƲ�����550�ֵ�5�����������ijɼ���������������Ϊ150�֣��ľ�Ҷͼ���������5�����������ijɼ��ķ����3���ڳɼ�������550�ֵ����п����г�ȡ2���������Ʒ����������ٳ鵽һ���������ĸ��ʣ� | [0��400] | [400��480] | [480��550] | [550��750] | |
| �Ŀƿ��� | 67 | 35 | 19 | 5 |
| ���ƿ��� | 53 | a | 41 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
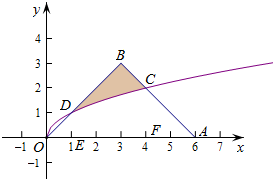 ��ͼ������������OAB�Ķ���A��B������ֱ�Ϊ��6��0������3��3������AB������y=$\sqrt{x}$���ڵ�C���ڡ�OAB����ȡһ��P�����P������Ӱ���ֵĸ���Ϊ��������
��ͼ������������OAB�Ķ���A��B������ֱ�Ϊ��6��0������3��3������AB������y=$\sqrt{x}$���ڵ�C���ڡ�OAB����ȡһ��P�����P������Ӱ���ֵĸ���Ϊ��������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{5}{27}$ | D�� | $\frac{11}{54}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com