
 某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.
某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.分析 (Ⅰ)根据题意利用列出方程,能求出a,b.
(Ⅱ)分别求出甲、乙两种数据的平均数和方差,得到$\overline{x_甲}=\overline{x_乙}$,$s_甲^2>s_乙^2$,从而得到应选派乙参加更合适.
(Ⅲ)设从甲同学的5次成绩中任取两次,利用列举法求出基本事件个数和“优秀组合”包含基本事件个数,由此能求出甲同学的两次成绩为“优秀组合”的概率.
解答 解:(Ⅰ)根据题意可知:
$\overline{x_甲}=\frac{1}{5}({87+88+90+92+90+a})=90$,
$\overline{x_乙}=\frac{1}{5}({89+90+91+92+80+b})=90$,
解得a=3,b=8.
(Ⅱ)$s_甲^2=\frac{1}{5}[{{{({87-90})}^2}+{{({88-90})}^2}+{{({90-90})}^2}+{{({92-90})}^2}+{{({93-90})}^2}}]=\frac{26}{5}$,
$s_乙^2=\frac{1}{5}[{{{({88-90})}^2}+{{({89-90})}^2}+{{({90-90})}^2}+{{({91-90})}^2}+{{({92-90})}^2}}]=2$,
∵$\overline{x_甲}=\overline{x_乙}$,$s_甲^2>s_乙^2$,
∴甲、乙两生的整体水平相当,乙生更稳定一些,
故应选派乙参加更合适.
(Ⅲ)设从甲同学的5次成绩中任取两次得基本事件有:
(87,88),(87,90),(87,92),(87,93),(88,90),(88,92),
(88,93),(90,92),(90,93),(92,93),共计10个,
而两次成绩的平均分大于90,即“优秀组合”包含的基本事件有:
(88,93),(90,92),(90,93),(92,93)共计4个,
所以甲同学的两次成绩为“优秀组合”的概率为$\frac{4}{10}=\frac{2}{5}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
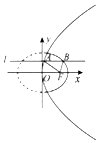 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )| A. | 3 | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | 2 | C. | $\frac{{\sqrt{5}+1}}{2}$或2 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{π}{2}+2kπ,\frac{3}{2}π+2kπ](k∈Z)$ | B. | $[kπ+\frac{π}{4},kπ+\frac{3}{4}π](k∈Z)$ | ||
| C. | [π+2kπ,3π+2kπ](k∈Z) | D. | $[kπ-\frac{π}{4},kπ+\frac{π}{4}](k∈Z)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com