
分析 (1)通过将点(n,2an+1-an)代入直线y=x,进而变形可知2(an+1-n-1+2)=an-n+2,从而可得结论;
(2)通过(1)可知an=n-2+$\frac{3}{{2}^{n}}$,利用分组求和法计算可知Sn=6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$,代入计算可知bn=1-$\frac{3}{{2}^{n+1}}$;
(3)通过代入、化简整理可知问题转化为n2-9n+8>$\frac{6}{{2}^{n}}$对n>k(k∈N+)恒成立,通过分析不等式两端的单调性即得结论.
解答 (1)证明:∵点(n,2an+1-an)(n∈N+)在直线y=x上,
∴2an+1-an=n,2an+1=an+n,
∴2(an+1-n-1+2)=an-n+2,
又∵a1-1+2=$\frac{1}{2}$-1+2=$\frac{3}{2}$,
∴数列{an-n+2}是首项为$\frac{3}{2}$、公比为$\frac{1}{2}$的等比数列;
(2)解:由(1)可知an-n+2=$\frac{3}{{2}^{n}}$,即an=n-2+$\frac{3}{{2}^{n}}$,
∴Sn=$\frac{n(n+1)}{2}$-2n+3•$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$,
bn=an+1-an-1=(n+1)-2+$\frac{3}{{2}^{n+1}}$-(n-2+$\frac{3}{{2}^{n}}$)=1-$\frac{3}{{2}^{n+1}}$;
(3)解:∵Sn-2bn>3n-4对n>k(k∈N+)恒成立,
∴(6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$)-2(1-$\frac{3}{{2}^{n+1}}$)>3n-4对n>k(k∈N+)恒成立,
整理得:n2-9n+8>$\frac{6}{{2}^{n}}$,
∵当n取不超过8的自然数时f(n)=n2-9n+8≤0,
当n≥9时f(n)随着n的增大而增大,且f(9)=8,
而g(n)=$\frac{6}{{2}^{n}}$随着n的增大而减小,且g(8)>0、g(9)<f(9),
∴k的最小值为8.
点评 本题是一道关于数列与不等式的综合题,涉及构造等比数列、数列的单调性等基础知识,注意解题方法的积累,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
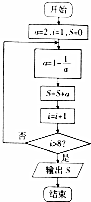
| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com