
设函数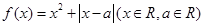 .
.
(1)讨论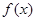 的奇偶性;
的奇偶性;
(2)当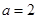 时,求
时,求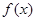 的单调区间;
的单调区间;
(3)若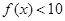 对
对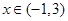 恒成立,求实数
恒成立,求实数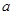 的取值范围.
的取值范围.
(1)当a=0是偶函数;当a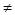 0时函数f(x)为非奇非偶函数
0时函数f(x)为非奇非偶函数
(2) 原函数的减区间为(-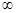 ,
,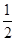 ),增区间为(
),增区间为(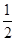 ,+
,+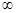 );(3)
);(3) 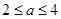
解析试题分析:解:(1)i)当a=0时:f(x)=x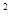 +
+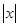
∵f(-x)="(-x)+" 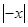 =x
=x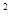 +
+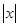 =f(x)
=f(x) 函数f(x)为偶函数3分
函数f(x)为偶函数3分
ii)当a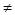 0时:
0时:
∵f(1)=1+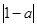 ,f(-1)=1+
,f(-1)=1+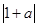
若f(1)=f(-1),则1+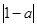 =1+
=1+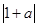 从而a=0,舍去;
从而a=0,舍去;
若f(1)=-f(-1),则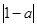 +
+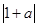 =-2从而a
=-2从而a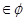
 f(1)
f(1)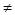 ±f(-1),
±f(-1), 函数f(x)为非奇非偶函数6分
函数f(x)为非奇非偶函数6分
(2)当a=2时:
f(x)=x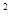 +
+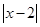 =
=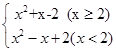
 原函数的减区间为(-
原函数的减区间为(-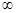 ,
,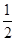 ),增区间为(
),增区间为(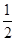 ,+
,+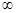 );10分
);10分
(3)∵x (-1,3)
(-1,3) f(x)<10可变为x
f(x)<10可变为x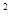 -10<a-x< 10-x
-10<a-x< 10-x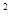
即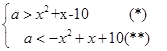
对(*):令g(x)= x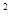 +x-10,其对称轴为
+x-10,其对称轴为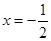
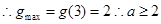 ③
③
对②令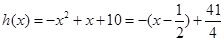
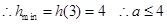 ④
④
由③、④知: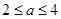 16分
16分
考点:函数性质的综合运用
点评:主要是考查了函数奇偶性和单调性以及函数的最值的运用,属于基础题。


科目:高中数学 来源: 题型:解答题
定义在[-1,1]上的奇函数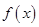 满足
满足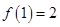 ,且当
,且当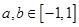 ,
,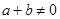 时,有
时,有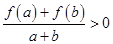 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若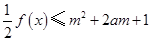 对所有
对所有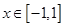 ,
,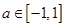 恒成立,
恒成立,
求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com