
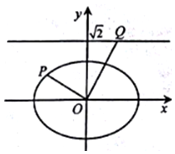
 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.分析 (1)由椭圆的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1,列出方程组,求出a,b,由此能求出椭圆的标准方程.
(2)当OP的斜率为0时,|OP|=$\sqrt{2}$,|OQ|=$\sqrt{2}$,$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=1;当OP的斜率不为0时,设直线OP的方程为y=kx,由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx}\end{array}\right.$,得(2k2+1)x2=2,由此利用直线与直线垂直、韦达定理,结合已知条件,求出$\frac{1}{{|OP{|^2}}}+\frac{1}{{|OQ{|^2}}}$=1.
解答 解:(1)∵椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1,
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{{a}^{2}}{c}-c=1}\end{array}\right.$,且a2=b2+c2,
解得a=$\sqrt{2}$,b=c=1.
∴椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)设P(x1,y1),Q(${x}_{2},\sqrt{2}$),
由题意知OP的斜率存在,
当OP的斜率为0时,|OP|=$\sqrt{2}$,|OQ|=$\sqrt{2}$,
∴$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=1,
当OP的斜率不为0时,设直线OP的方程为y=kx,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx}\end{array}\right.$,得(2k2+1)x2=2,
解得${{x}_{1}}^{2}=\frac{2}{2{k}^{2}+1}$,∴${{y}_{1}}^{2}=\frac{2{k}^{2}}{2{k}^{2}+1}$,
∴|OP|2=${{x}_{1}}^{2}+{{y}_{1}}^{2}$=$\frac{2{k}^{2}+2}{2{k}^{2}+1}$,
∵OP⊥OQ,∴直线OQ的方程为y=-$\frac{1}{k}x$,
由$\left\{\begin{array}{l}{y=\sqrt{2}}\\{y=-\frac{1}{k}x}\end{array}\right.$,得${x}_{2}=-\sqrt{2}k$,
∴|OQ|2=${{x}_{2}}^{2}+(\sqrt{2})^{2}=2{k}^{2}+2$,
∴$\frac{1}{{|OP{|^2}}}+\frac{1}{{|OQ{|^2}}}$=$\frac{2{k}^{2}+1}{2{k}^{2}+2}+\frac{1}{2{k}^{2}+2}$=1.
综上,$\frac{1}{{|OP{|^2}}}+\frac{1}{{|OQ{|^2}}}$=1.
点评 本题考查椭圆方程的求法,考查线段平方的倒数和的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
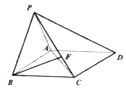 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{8}$ | C. | $-\frac{3}{8}$ | D. | $-\frac{15}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
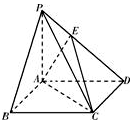 四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$
四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -32 | B. | -16 | C. | -10 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com