
以椭圆 +
+ =1的焦点为焦点,以直线
=1的焦点为焦点,以直线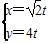 为渐近线的双曲线的参数方程为________________.
为渐近线的双曲线的参数方程为________________.
科目:高中数学 来源: 题型:
数列{an}中,已知a1=1,当n≥2时,an-an-1=2n-1,依次计算a2、a3、a4后,猜想an的表达式是( )
A.an=3n-2 B.an=n2
C.an=3n-1 D.an=4n-3
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A、B,C、D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E、F,点M在EF上,且∠BAD=∠BMF.
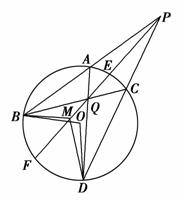
(1)求证:PA·PB=PM·PQ;
(2)求证:∠BMD=∠BOD.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线C1: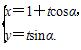 (t为参数),圆C2:ρ=1.(极坐标轴与x轴非负半轴重合)
(t为参数),圆C2:ρ=1.(极坐标轴与x轴非负半轴重合)
(1)当α=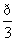 时,求直线C1被圆C2所截得的弦长;
时,求直线C1被圆C2所截得的弦长;
(2)过坐标原点O作C1的垂线,垂足为A.当a变化时,求A点的轨迹的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线C1: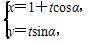 (t为参数),圆C2:
(t为参数),圆C2: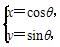 (θ为参数).
(θ为参数).
(1)当α=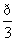 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(2)过坐标原点O作C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M={x||2x-1|<2},N=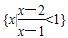 ,则M∩N等于( )
,则M∩N等于( )
A.{x|1<x<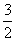 } B.{x|
} B.{x| <x<1}
<x<1}
C.{x|- <x<
<x<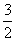 } D.{x|-
} D.{x|- <x<
<x<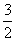 ,且x≠1}
,且x≠1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com