
分析 取AB中点O,连结AO、CO,推导出SO=1,CO=3,∠SOC是二面角S-AB-C的平面角,由此利用余弦定理能求出SC的长.
解答 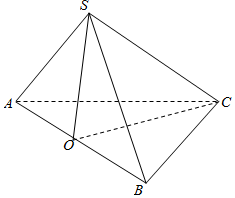 解:取AB中点O,连结AO、CO,
解:取AB中点O,连结AO、CO,
∵三棱锥S-ABC中,正三角形ABC的边长为$2\sqrt{3}$,SA=SB=2,
∴SO⊥AB,CO⊥AB,
且SO=$\sqrt{S{A}^{2}-O{A}^{2}}$=$\sqrt{4-3}=1$,
CO=$\sqrt{B{C}^{2}-B{O}^{2}}$=$\sqrt{12-3}$=3,
∴∠SOC是二面角S-AB-C的平面角,
∵二面角S-AB-C的平面角的大小为60°,
∴∠SOC=60°,
∴SC=$\sqrt{S{O}^{2}+C{O}^{2}-2×SO×CO×cos60°}$
=$\sqrt{1+9-2×1×3×\frac{1}{2}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
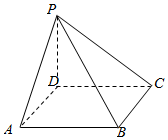 已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (0,3] | C. | (0,3) | D. | (-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | 3π | C. | $\frac{π}{6}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
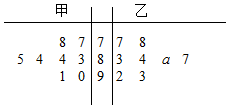 将甲、乙两名同学8次数学测验成绩统计如茎叶图所示,若乙同学8次数学测试成绩的中位数比甲同学8次数学测验成绩的平均数多1,则a=( )
将甲、乙两名同学8次数学测验成绩统计如茎叶图所示,若乙同学8次数学测试成绩的中位数比甲同学8次数学测验成绩的平均数多1,则a=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com