
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,椭圆上的点到焦点的最大距离为3.
,椭圆上的点到焦点的最大距离为3.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 两点均在
两点均在![]() 轴的左侧,记
轴的左侧,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)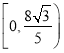 .
.
【解析】
(1)根据直线![]() 的倾斜角为
的倾斜角为![]() 可得
可得![]() ,椭圆上的点到焦点的最大距离为3,可得
,椭圆上的点到焦点的最大距离为3,可得![]() ,再结合
,再结合![]() 可解得
可解得![]() ,
,![]() ,从而可得椭圆
,从而可得椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)①当直线![]() 斜率不存在时,
斜率不存在时,![]() ;②当直线
;②当直线![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,
,![]() ,
,![]() ,显然的
,显然的![]() ,
,![]() 同号,联立
同号,联立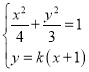 ,根据韦达定理求得
,根据韦达定理求得![]()
 ,再根据函数
,再根据函数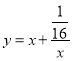 在
在![]() 上单调递增可求得
上单调递增可求得![]() ,进一步求得
,进一步求得![]() .
.
(1)因为椭圆方程为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,
,
所以在![]() 中(
中(![]() 为坐标原点),
为坐标原点),![]() ,所以
,所以![]() ,
,
因为椭圆上的点到焦点的最大距离为3,
所以![]() ,所以
,所以![]() .
.
因为![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)①当直线![]() 斜率不存在时,直线方程为
斜率不存在时,直线方程为![]() ,
,
此时![]() ,
,![]() ,
,![]() 与
与![]() 的面积相等,
的面积相等,![]() .
.
②当直线![]() 斜率存在时,因为
斜率存在时,因为![]() ,
,![]() 两点均在
两点均在![]() 轴的左侧,
轴的左侧,
设直线方程为![]() ,
,![]() ,
,![]() ,显然的
,显然的![]() ,
,![]() 同号,
同号,
由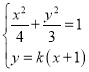 ,得
,得![]() ,
,
显然![]() ,方程有实根,
,方程有实根,
由韦达定理知的![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 或
或![]() ,
,
此时![]()

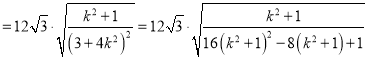

因为![]() 或
或![]() ,所以
,所以![]() .
.
因为函数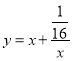 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以![]() ,
,
所以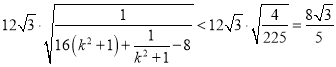 .
.
当直线![]() 的斜率存在时,
的斜率存在时,![]() .
.
综上所述,![]() 的取值范围为
的取值范围为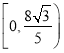 .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):

已知![]() 三类工种职工每人每年需交的保费分别为25元25元40元,出险后的赔偿金额分别为100万元100万元50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年需交的保费分别为25元25元40元,出险后的赔偿金额分别为100万元100万元50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)设A类工种职工的每份保单保险公司的收益为随机变量X(元),求X的数学期望;
(2)若该公司全员参加保险,求保险公司该业务所获利润的期望值;
(3)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,若出意外,企业自行拿出与保险公司提供的等额赔偿金赔付给出意外职工,且企业开展这项工作每年还需另外固定支出12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 相交所得的线段长为3,椭圆的左、右焦点分别为
相交所得的线段长为3,椭圆的左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com