练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．四面体ABCD的对边长分别相等，AB=CD=a，AC=BD=b，AD=BC=c，求这个四面体外接球的直径．

    分析 构造长方体，使得面上的对角线长分别为a，b，c，则长方体的对角线长等于四面体外接球的直径．

    解答 解：∵四面体ABCD的对边长分别相等，AB=CD=a，AC=BD=b，AD=BC=c，
    ∴构造长方体，使得面上的对角线长分别为a，b，c，
    则长方体的对角线长等于四面体外接球的直径．
    设长方体的棱长分别为x，y，z，则x2+y2=a2，y2+z2=b2，x2+z2=c2，
    ∴四面体外接球的直径为$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{2}}$．

    点评 本题考查球内接多面体，考查学生的计算能力，构造长方体，利用长方体的对角线长等于四面体外接球的直径是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．若向量$\overrightarrow{m}$，$\overrightarrow{n}$的夹角为45°，且|$\overrightarrow{m}$|=l，|2$\overrightarrow{m}$-$\overrightarrow{n}$|=$\sqrt{10}$，则|$\overrightarrow{n}$|=3$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．二元一次方程组$\left\{{\begin{array}{l}{{a_1}x+{b_1}y={c_1}}\\{{a_2}x+{b_2}y={c_2}}\end{array}}\right.$存在唯一解的必要非充分条件是（　　）
    A．系数行列式D≠0
    B．比例式$\frac{a_1}{a_2}≠\frac{b_1}{b_2}$
    C．向量$（{\begin{array}{l}{a_1}\\{{a_2}}\end{array}}），（{\begin{array}{l}{b_1}\\{{b_2}}\end{array}}）$不平行
    D．直线a1x+b1y=c1，a2x+b2y=c2不平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在△ABC中，角A、B、C的对边分别是a、b、c．已知（2a-c）cosB=bcosC．
    （1）求角B的值；
    （2）若a=1，c=2，求b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知Sn是数列{an}的前n项和，若Sn=1-nan（n=1，2，3，…），则Sn关于n的表达式为Sn=$\frac{n}{n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．2004年5月31日国家制定了新的酒驾醉驾标准，车辆驾驶人员血液酒精含量大于或等于20mg/100ml（0.2‰），小于80mg/100ml（0.8‰）为饮酒驾车；大于或等于80mg/100ml（0.8‰）为醉酒驾车．以下是血清里酒精含量与常人精神状态关联的五个阶段：
    血清酒精含量[0.2‰，0.4‰）[0.4‰，0.8‰）[0.8‰，1.2‰）[1.2‰，1.6‰）[1.6‰，+∞）
    常人精神状态君子态（愉快）孔雀态（炫耀）狮子态（打架）猴子态（失控）狗熊态（昏睡）
    但血清中的酒精含量在饮用等量酒的情况下，是因人而异有所不同的．下面是某卫生机构在20～55岁的饮酒男性志愿者中，随机选取30人作为样本进行测试．在饮用了250ml（60%）60度纯粮白酒（相当于5瓶啤酒）恰好一小时，血清中酒精含量（最大值）统计数据：
    血清酒精含量[0.2，0.4‰‰）[0.4‰，0.8‰）[0.8‰，1.2‰）[1.2‰，1.6‰）[1.6‰，+∞）
    人数1212132
    以上数据为参考依据．
    （1）试估计20～55岁的饮酒男性在饮用了250ml（60%）60度纯粮白酒（相当于5瓶啤酒）恰好一小时，血清中酒精含量0.8%及以上的概率是多少？
    （2）在午夜12点，酒吧营业两小时，客人餐饮大约一小时．有5名20～55岁的男性（每人饮用相当于60度纯粮白酒饮酒量250ml左右）从酒吧走出并驾车离开（已知其中4人血清酒精含量0.8‰及以上，一人0.8‰以下），恰有两人途中被交警拦截检查，则这两人均是醉酒驾车的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．$\root{4}{4}$÷$\root{4}{64}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，且|$\overrightarrow{b}$|=2，$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影是-1，$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是-3，$\overrightarrow{BD}$=λ$\overrightarrow{BA}$．
    （1）求$\overrightarrow{a}$•$\overrightarrow{b}$；
    （2）若λ=$\frac{1}{3}$，求|$\overrightarrow{OD}$|；
    （3）若OD⊥BA，求λ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

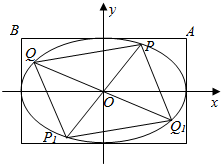    7．已知椭圆C的中心在原点，左焦点为F1（-1，0），右准线方程为：x=4
    （1）求椭圆C的标准方程；
    （2）若椭圆C上点N到定点M（m，0）（0＜m＜2）的距离的最小值为1，求m的值及点N的坐标；
    （3）分别过椭圆C的四个顶点作坐标轴的垂线，围成如图所示的矩形，A、B是所围成的矩形在x轴上方的两个顶点．若P、Q是椭圆C上两个动点，直线OP、OQ与椭圆的另一交点分别为P1、Q1，且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积，试探求四边形PQP1Q1的面积是否为定值，并说明理由．

    查看答案和解析>>

    同步练习册答案