
分析 由向量运算可得R为AC的一个三等分点,由已知数据可得cos∠BAD=$\frac{11}{24}$,可求$|\overrightarrow{AC}|$,可得答案.
解答 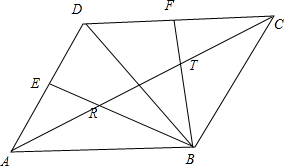 解:由题意可得$\overrightarrow{AR}$=$\overrightarrow{AB}$+$\overrightarrow{BR}$=$\overrightarrow{AB}$+λ$\overrightarrow{BE}$
解:由题意可得$\overrightarrow{AR}$=$\overrightarrow{AB}$+$\overrightarrow{BR}$=$\overrightarrow{AB}$+λ$\overrightarrow{BE}$
=$\overrightarrow{AB}$+λ($\overrightarrow{AE}$-$\overrightarrow{AB}$)=$\overrightarrow{AB}$+λ($\frac{1}{2}$$\overrightarrow{AD}$-$\overrightarrow{AB}$)
=(1-λ)$\overrightarrow{AB}$+$\frac{1}{2}$λ$\overrightarrow{AD}$,
又A、R、C共线,∴$\overrightarrow{AR}$=t$\overrightarrow{AC}$
=t($\overrightarrow{AB}$+$\overrightarrow{AD}$)=t$\overrightarrow{AB}$+t$\overrightarrow{AD}$,
∴$\left\{\begin{array}{l}{1-λ=t}\\{\frac{1}{2}λ=t}\end{array}\right.$,解得t=$\frac{1}{3}$,
即R为AC的一个三等分点,∴|$\overrightarrow{AR}$|=$\frac{1}{3}$$|\overrightarrow{AC}|$,
∵AB=4,AD=3,BD=$\sqrt{14}$,
又∵$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$,∴$\overrightarrow{BD}$2=($\overrightarrow{AD}$-$\overrightarrow{AB}$)2,
∴14=16+9-2×4×3×cos∠BAD,解得cos∠BAD=$\frac{11}{24}$
∴$|\overrightarrow{AC}|$2=($\overrightarrow{AD}$+$\overrightarrow{AB}$)2=16+9+2×4×3×cos∠BAD=36,
∴$|\overrightarrow{AC}|$=6,∴|$\overrightarrow{AR}$|=$\frac{1}{3}$$|\overrightarrow{AC}|$=2
故答案为:2
点评 本题考查平面向量的数量积,涉及平面向量基本定理和向量的共线以及模长公式,属中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,且PD=PC=BC=3,CD=3$\sqrt{2}$,E为PB中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,且PD=PC=BC=3,CD=3$\sqrt{2}$,E为PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.试确定x,y,p,q的值,并补全频率分布直方图.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.试确定x,y,p,q的值,并补全频率分布直方图. | 网购金额 (单位:元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.30 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com