Question

1．已知正方形ABCD，E、F分别是CD、AD的中点．BE、CF交于点P．求证：（1）BE⊥CF；（2）AP=AB．

Answer 1

分析 （1）连接BF，由已知推导出△BCE≌△CDF，从而∠PCE+∠CEP=90°，由此能证明BE⊥CF．
（2）先推导出点A、B、P、F四点共圆，从而∠AFB=∠APB，再由△ABF≌△BCE，推导出∠APB=∠ABP，由此能证明AP=AB．

解答 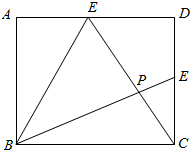证明：（1）连接BF，
∵E、F分别是正方形ABCD的边CD和AD的中点，
∴BC=CD，∠BCE=∠CDF，CE=DF，
∴△BCE≌△CDF，
∴∠CBE=∠FCD，∠BEC=∠CFD，
∴∠PCE+∠CEP=∠DCE+∠CFD=90°，
∴BE⊥CF．
（2）∵BE⊥CF，∴∠FPB=90°，又∠DAB=90°，
∴点A、B、P、F四点共圆，∴∠AFB=∠APB，
∵AB=BC，∠ABF=∠BCE，AF=CE，
∴△ABF≌△BCE，
∴90°-∠CBE=90°-∠ABF，即∠ABP=∠AFB，
∴∠APB=∠ABP，∴AP=AB．

点评 本题考查两直线垂直和两线段相等的证明，是中档题，解题时要认真审题，注意四点共圆和三角形全等的性质的合理运用．