
分析 由题意求出函数的周期,根据函数的周期性求出函数在[2015,2016]的单调性,转化f(2015)=-f(1),从而求出函数的闭区间上的最大值即可.
解答 解:∵己知定义在R上的奇函数f(x)的图象为一条连续不断的曲线,
∴f(-x)=-f(x),
∵f(x+1)=f(1-x),
∴f(x+2)=f[(x+1)+1]=f[1-(x+1)]=f(-x)=-f(x),
即f(x+2)=-f(x),
f(x+4)=-f(x+2),
∴f(x+4)=f(x),
∴函数的周期为4,
0<x<1时,f(x)的导函数f′(x)满足:f′(x)<0,
∴f(x)在(0,1)递减,f(x)在[2015,2016]递减,
∴f(2015)=f(4×504-1)=f(-1)=-f(1),
∵f(1)=a,
∴f(2015)=-f(1)=-a,
故f(x)在[2015,2016]上的最大值为为:f(2015)=-a,
故答案为:-a.
点评 本题考查函数的奇偶性、周期性的应用,函数值的求法以及函数的单调性问题,考查计算能力,是一道中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
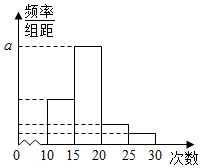 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9\sqrt{5}}{20}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com