
分析 (Ⅰ)分类讨论,求不等式f(x)≥4的解集;
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求出f(x)最小值为$|{\frac{5}{2}-a}|$,从而$|{\frac{5}{2}-a}|≥a$,解得$a≤\frac{5}{4}$,即可求实数a的最大值.
解答 解:(Ⅰ)$f(x)=|{x-\frac{5}{2}}|+|{x+\frac{1}{2}}|$=$\left\{\begin{array}{l}-2x+2,x<-\frac{1}{2}\\ 3,-\frac{1}{2}≤x≤\frac{5}{2}\\ 2x-2,x>\frac{5}{2}\end{array}\right.$
由f(x)≥4得$\left\{\begin{array}{l}x<-\frac{1}{2}\\-2x+2≥4\end{array}\right.$或$\left\{\begin{array}{l}x>\frac{5}{2}\\ 2x-2≥4\end{array}\right.$,解得x≤-1或x≥3,
所以不等式的解集为{x|x≤1或x≥3};
(Ⅱ)由绝对值的性质得$f(x)=|{x-\frac{5}{2}}|+|{x-a}|≥$$|{({x-\frac{5}{2}})-({x-a})}|=|{a-\frac{5}{2}}|$,
所以f(x)最小值为$|{\frac{5}{2}-a}|$,从而$|{\frac{5}{2}-a}|≥a$,解得$a≤\frac{5}{4}$,因此a的最大值为$\frac{5}{4}$.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±512 | B. | 512 | C. | ±1024 | D. | 1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|0≤x≤2} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
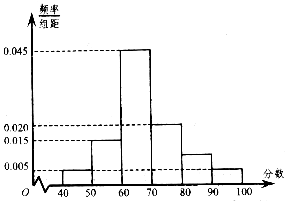 上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.
上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2 | B. | 2:5 | C. | 1:3 | D. | 4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com