已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的长轴长为$2\sqrt{2}$.离心率$e=\frac{{\sqrt{2}}}{2}$．(Ⅰ)求椭圆G的方程,(Ⅱ)设过椭圆G的上顶点A的直线l与椭圆G的另一个交点为B.与x轴交于点C.线段AB的中点为D.线段AB的垂直平分线分别交x轴.y轴于P.Q两点．问:是否存在直线l使△PDC与△POQ的� 题目和参考答案——青夏教育精英家教网—

9．

已知椭圆$G：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为$2\sqrt{2}$，离心率$e=\frac{{\sqrt{2}}}{2}$．
（Ⅰ）求椭圆G的方程；
（Ⅱ）设过椭圆G的上顶点A的直线l与椭圆G的另一个交点为B，与x轴交于点C，线段AB的中点为D，线段AB的垂直平分线分别交x轴、y轴于P、Q两点．问：是否存在直线l使△PDC与△POQ的面积相等（O为坐标原点）？若存在，求出所有满足条件的直线l的方程；若不存在，说明理由．

分析（Ⅰ）由题意可得2a=2$\sqrt{2}$，即a=$\sqrt{2}$，e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，可得c，再由a，b，c的关系可得b，进而得到椭圆方程；
（Ⅱ）设A（0，1），直线AB的方程为y=kx+1，代入椭圆方程，求得B的坐标，再由中点坐标公式可得D，求得线段AB的中垂线方程，可得P，Q的坐标，假设存在直线l，使△PDC与△POQ的面积相等（O为坐标原点），运用三角形的面积公式，$\frac{PC}{PO}$=$\frac{PQ}{PD}$，即有$\frac{{x}_{C}-{x}_{P}}{-{x}_{P}}$=$\frac{{x}_{Q}-{x}_{P}}{{x}_{D}-{x}_{P}}$，解方程即可得到所求k的值，进而判断存在直线l．

解答解：（Ⅰ）由题意可得2a=2$\sqrt{2}$，即a=$\sqrt{2}$，e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，解得c=1，b=1，
可得椭圆的方程为$\frac{{x}^{2}}{2}$+y²=1；
（Ⅱ）设A（0，1），直线AB的方程为y=kx+1，
代入椭圆方程，可得（1+2k²）x²+4kx=0，
解得x=-$\frac{4k}{1+2{k}^{2}}$，或x=0．
即有B（-$\frac{4k}{1+2{k}^{2}}$，$\frac{1-2{k}^{2}}{1+2{k}^{2}}$），C（-$\frac{1}{k}$，0），
中点D的坐标为（-$\frac{2k}{1+2{k}^{2}}$，$\frac{1}{1+2{k}^{2}}$），
可得AB的中垂线方程为y-$\frac{1}{1+2{k}^{2}}$=-$\frac{1}{k}$（x+$\frac{2k}{1+2{k}^{2}}$），
化为y=-$\frac{1}{k}$x-$\frac{1}{1+2{k}^{2}}$，
可得P（-$\frac{k}{1+2{k}^{2}}$，0），Q（0，-$\frac{1}{1+2{k}^{2}}$），
假设存在直线l，使△PDC与△POQ的面积相等（O为坐标原点），
即有$\frac{1}{2}$PD•PC•sin∠DPC=$\frac{1}{2}$PO•PQ•sin∠OPQ，
即有PD•PC=PO•PQ，
即为$\frac{PC}{PO}$=$\frac{PQ}{PD}$，即有$\frac{{x}_{C}-{x}_{P}}{-{x}_{P}}$=$\frac{{x}_{Q}-{x}_{P}}{{x}_{D}-{x}_{P}}$，
即有$\frac{-1-{k}^{2}}{{k}^{2}}$=-1，
可得k无解．
故不存在直线l，使△PDC与△POQ的面积相等（O为坐标原点）．

点评本题考查椭圆的方程的求法，注意运用椭圆的离心率公式和长轴长，考查直线方程和椭圆方程联立，求交点，两直线垂直的条件及中点坐标公式的运用，考查化简整理的运算能力，属于中档题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

17．函数f（x）=x³+sinx+2016（x∈R），若f（a）=2015，则f（-a）=2017．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．已知a，b为实数，则“a³＜b³”是“2^a＜2^b”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分又不必要条件

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．已知：z₁，z₂∈C，求证：（$\overline{\frac{{z}_{1}}{{z}_{2}}}$）=$\frac{\overline{{z}_{1}}}{\overline{{z}_{2}}}$（z₂≠0）

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．已知F₁，F₂分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右两个焦点，若在双曲线C上存在点P使∠F₁PF₂=90°，且满足2∠PF₁F₂=∠PF₂F₁，那么双曲线C的离心率为（　　）

A．

$\sqrt{3}$+1

B．

C．

$\sqrt{3}$

D．

$\frac{\sqrt{5}}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

14．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F₁，F₂，点P在椭圆上，O为坐标原点，若|OP|=$\frac{1}{2}$|F₁F₂|，且|PF₁|•|PF₂|=a²，则该椭圆的离心率为（　　）

A．

$\frac{3}{4}$

B．

$\frac{\sqrt{3}}{2}$

C．

$\frac{\sqrt{2}}{2}$

D．

$\frac{1}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．函数$f（x）=\left\{{\begin{array}{l}{{{（x-1）}^2}，x≥0}\\{|{{e^x}-2}|，x＜0}\end{array}}\right.$则f（-1）=2-$\frac{1}{e}$，若方程f（x）=m有两个不同的实数根，则m的取值范围为（0，2）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．运行如图所示的程序框图，则输出的结果是（　　）

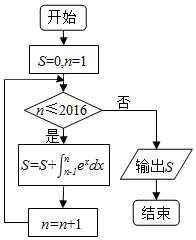
A．

e²⁰¹⁶-e²⁰¹⁵

B．

e²⁰¹⁷-e²⁰¹⁶

C．

e²⁰¹⁵-1

D．

e²⁰¹⁶-1

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．两组学校的社会实践活动各有7位人员（下文分别简称为“甲小组”和“乙小组”）．两小组成员分别独立完成一项社会调查，并形成调查报告，每位成员从启动调查到完成报告所用的时间（单位：天）如表所示：

组别	每位成员从启动调查到完成报告所用的时间（单位：天）
甲小组	10	11	12	13	14	15	16
乙小组	12	13	15	16	17	14	a

假设所有成员所用时间相互了独立，从甲、乙两小组随机各选1人，甲小组选出的人记为A，乙小组选出的人记为B．
（Ⅰ）求A所用时间不小于13天的概率；
（Ⅱ）如果a=18，求A所用的时间比B所用时间长的概率．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学