
| A. | (-$\frac{10}{3}$,-2) | B. | (-∞,-2) | C. | -$\frac{34}{15}$<t<-2 | D. | (-1,2) |
分析 求出函数f(x)的导数,判断函数的单调性和极值,利用换元法设|f(x)|=m,转化为一元二次函数根的分布进行求解即可.
解答  解:$f(x)=\frac{1}{3}{x^3}+{x^2}-3x,f'(x)={x^2}+2x-3=0$,
解:$f(x)=\frac{1}{3}{x^3}+{x^2}-3x,f'(x)={x^2}+2x-3=0$,
得x=-3,x=1,
由f′(x)>0得x>1或x<-3,即函数在(-∞,-3),(1,+∞)单调递增,
由f′(x)<0得-3<x<1,则函数在(-3,1)单调递减,
则函数的极大值为f(-3)=9,函数的极小值为$f(1)=-\frac{5}{3}$,
根据函数的图象可知,
设|f(x)|=m,可知m2+tm+1=0,原方程有12个不同的根,
则m2+tm+1=0方程应在$(0,\frac{5}{3})$内有两个不同的根,
设h(m)=m2+tm+1,
则$\left\{{\begin{array}{l}{h(\frac{5}{3})>0}\\{0<-\frac{t}{2}<\frac{5}{3}}\\{△={t^2}-4>0}\end{array}}\right.⇒-\frac{34}{15}<t<-2$,
所以取值的范围$-\frac{34}{15}<t<-2$.
故选:C
点评 本题主要考查函数与方程的应用,求函数的导数判断函数的极值和单调性,以及利用换元法转化为一元二次函数是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{e}$,1) | B. | (-∞,$\frac{1}{e}$) | C. | (-1,+∞) | D. | (-$\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
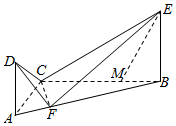 如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF,D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.
如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF,D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
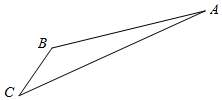 如图,旅客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从A乘缆车到B,再从B匀速步行到C.假设缆车匀速直线运动的速度为130米/分钟,山路AC长1260米,经测量,cosA=$\frac{12}{13}$,cosC=$\frac{3}{5}$.
如图,旅客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从A乘缆车到B,再从B匀速步行到C.假设缆车匀速直线运动的速度为130米/分钟,山路AC长1260米,经测量,cosA=$\frac{12}{13}$,cosC=$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com