Question

9．阅读如图的程序框图，当该程序运行后输出的S值是（　　）

• A． $\frac{3}{5}$
• B． $\frac{5}{8}$
• C． $\frac{8}{13}$
• D． $\frac{13}{21}$

Answer 1

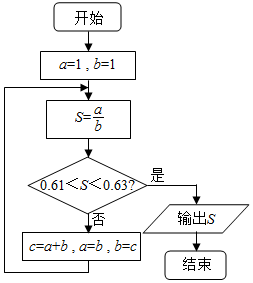
分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

解答 解：第一次执行循环体后：S=1，不满足退出循环的条件，c=2，a=1，b=2，
第二次执行循环体后：S=$\frac{1}{2}$，不满足退出循环的条件，c=3，a=2，b=3，
第三次执行循环体后：S=$\frac{2}{3}$，不满足退出循环的条件，c=5，a=3，b=5，
第四次执行循环体后：S=$\frac{3}{5}$，不满足退出循环的条件，c=8，a=5，b=8，
第五次执行循环体后：S=$\frac{5}{8}$，满足退出循环的条件，
故输出的S值为：$\frac{5}{8}$，
故选：B

点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．