
分析 (1)利用导数求出x=0处的切线斜率,根据点斜式写出切线方程;
(2)函数f(x)在(-3,0)上单调递减,即当x∈(-3,0)时,x2+2x-a≤0恒成立.要使得“当x∈(-3,0)时,x2+2x-a≤0恒成立”,等价于$\left\{{\begin{array}{l}{g(-3)≤0}\\{g(0)≤0}\end{array}}\right.$即$\left\{{\begin{array}{l}{a≥3}\\{a≥0}\end{array}}\right.$所以a≥3.
(3)根据函数的单调性,得出函数f(x)的最小值只能在${x_2}=-1+\sqrt{a+1}$处取得.
解答 解:由题意可知f'(x)=ex(x2+2x-a).
(Ⅰ)因为a=1,则f(0)=-1,f'(0)=-1,
所以函数f(x)在点(0,f(0))处的切线方程为y-(-1)=-(x-0).
即x+y+1=0.
(Ⅱ)因为函数f(x)在(-3,0)上单调递减,
所以当x∈(-3,0)时,f'(x)=ex(x2+2x-a)≤0恒成立.
即当x∈(-3,0)时,x2+2x-a≤0恒成立.
显然,当x∈(-3,-1)时,函数g(x)=x2+2x-a单调递减,
当x∈(-1,0)时,函数g(x)=x2+2x-a单调递增.
所以要使得“当x∈(-3,0)时,x2+2x-a≤0恒成立”,
等价于$\left\{{\begin{array}{l}{g(-3)≤0}\\{g(0)≤0}\end{array}}\right.$即$\left\{{\begin{array}{l}{a≥3}\\{a≥0}\end{array}}\right.$所以a≥3.
(Ⅲ)设g(x)=x2+2x-a,则△=4+4a.
①当△=4+4a≤0,即a≤-1时,g(x)≥0,所以f'(x)≥0.
所以函数f(x)在(-∞,+∞)单增,所以函数f(x)没有最小值.
②当△=4+4a>0,即a>-1时,令f'(x)=ex(x2+2x-a)=0得x2+2x-a=0,
解得${x_1}=-1-\sqrt{a+1},{x_2}=-1+\sqrt{a+1}$
随着x变化时,f(x)和f'(x)的变化情况如下:
| x | $(-∞,-1-\sqrt{1+a})$ | $-1-\sqrt{1+a}$ | $(-1-\sqrt{1+a},-1+\sqrt{1+a})$ | $-1+\sqrt{1+a}$ | $(-1+\sqrt{1+a},+∞)$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
点评 本题主要考查了利用导数求某点处的切线方程,函数的最值与单调性判断等综合知识点,属中等题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | a32+a72>a42+a62 | B. | a32+a72<a42+a62 | ||
| C. | a32+a72=a42+a62 | D. | a32+a72与a42+a62的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
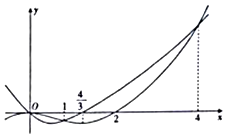
| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | $({0,\frac{4}{3}})$ | D. | (0,1),(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{\sqrt{2}}{2}$或$\frac{3\sqrt{13}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+$\frac{1}{a}$>2 | B. | a+$\frac{1}{a}$≥2 | C. | a+$\frac{1}{a}$≤-2 | D. | |a+$\frac{1}{a}$|≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}3-{x^2},x∈[-1,2]\\ x-3,x∈(2,5].\end{array}$
已知函数f(x)=$\left\{\begin{array}{l}3-{x^2},x∈[-1,2]\\ x-3,x∈(2,5].\end{array}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com