
���� ��1���������⣬����n�ζ����ظ�ʵ��ĸ��ʹ�ʽ��������ĸ���ֵ��
��2��������֪X�����п���ȡֵ�������Ӧ�ĸ���ֵ��
�Ӷ�д��X�ķֲ��У������ѧ����ֵ��
��� �⣺��1�������⣬��4�����У�ÿ����ȥ�Ա�������ĸ���Ϊ$\frac{1}{3}$��
ȥ����������ĸ���Ϊ$\frac{2}{3}$��
�衰��4������ǡ��i����ȥ�Ա������Ϊ�¼�Ai��i=0��1��2��3��4����
��$P��{A_i}��=C_4^i{��\frac{1}{3}��^i}{��\frac{2}{3}��^{4-i}}����i=0��1��2��3��4��$��
��4�˸�����ǡ��1��ȥ�Ա�������ĸ���Ϊ
$P��{A_1}��=C_4^1��\frac{1}{3}��{��\frac{2}{3}��^3}=\frac{32}{81}$������4�֣�
��2������֪��X�����п���ȡֵΪ0��3��4������5�֣�
$P��X=0��=P��{A_0}��+P��{A_4}��=C_4^0{��\frac{2}{3}��^4}+C_4^4{��\frac{1}{3}��^4}=\frac{17}{81}$������7�֣�
$P��X=3��=P��{A_1}��+P��{A_3}��=C_4^1��\frac{1}{3}��{��\frac{2}{3}��^3}+C_4^3{��\frac{1}{3}��^3}��\frac{2}{3}��=\frac{40}{81}$������9�֣�
$P��X=4��=P��{A_2}��=C_4^2{��\frac{1}{3}��^2}{��\frac{2}{3}��^2}=\frac{24}{81}$������11�֣�
��X�ķֲ���Ϊ��
| X | 0 | 3 | 4 |
| P | $\frac{17}{81}$ | $\frac{40}{81}$ | $\frac{24}{81}$ |
���� ���⿼������ɢ����������ķֲ�������ѧ�����ļ������⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | $2\sqrt{6}$ | C�� | $2\sqrt{3}$ | D�� | $\root{3}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -9 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��3 | B�� | -3��-3i | C�� | -3��3 | D�� | -3��3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0������$\frac{��}{2}$����sin ����tan �� | |
| B�� | �����ǵڶ����ǣ���$\frac{��}{2}$Ϊ��һ���ǻ�������� | |
| C�� | ���Ǧ����ձ߹���P��3k��4k����k��0����sin ��=$\frac{4}{5}$ | |
| D�� | ����=-$\frac{��}{3}$����cos ��=$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
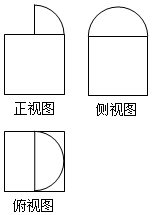 һ���������������ͼ��ͼ��ʾ�����в���ͼ��һ����Բ��߳�Ϊ2�������Σ�����ͼ��һ����Բ�����ڱ߳�Ϊ2�������Σ���û�����������Ϊ��������
һ���������������ͼ��ͼ��ʾ�����в���ͼ��һ����Բ��߳�Ϊ2�������Σ�����ͼ��һ����Բ�����ڱ߳�Ϊ2�������Σ���û�����������Ϊ��������| A�� | $8+\frac{��}{3}$ | B�� | $8+\frac{��}{4}$ | C�� | $8+\frac{4��}{3}$ | D�� | $4+\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com