Question

14．已知点A（-3，-$\frac{{\sqrt{6}}}{2}$）是抛物线C：y²=2px（p＞0）准线上的一点，点F是C的焦点，点P在C上且满足|PF|=m|PA|，当m取最小值时，点P恰好在以原点为中心，F为焦点的双曲线上，则该双曲线的离心率为（　　）

• A． 3
• B． $\frac{3}{2}$
• C． $\sqrt{2}+1$
• D． $\frac{{\sqrt{2}+1}}{2}$

Answer 1

分析 过P作准线的垂线，垂足为N，则由抛物线的定义，结合||PF|=m|PA|，可得$\frac{|PN|}{|PA|}$=m，设PA的倾斜角为α，则当m取得最小值时，cosα最小，此时直线PA与抛物线相切，求出P的坐标，利用双曲线的定义，即可求得双曲线的离心率．

解答 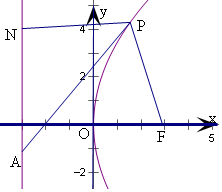解：点A（-3，-$\frac{{\sqrt{6}}}{2}$）是抛物线C：y²=2px（p＞0）
准线x=-$\frac{p}{2}$上的一点，
可得-$\frac{p}{2}$=-3，即p=6，
则抛物线的标准方程为y²=12x，
则抛物线的焦点为F（3，0），准线方程为x=-3，
过P作准线的垂线，垂足为N，
则由抛物线的定义可得|PN|=|PF|，
∵|PF|=m|PA|，
∴|PN|=m|PA|，则$\frac{|PN|}{|PA|}$=m，
设PA的倾斜角为α，则cosα=m，
当m取得最小值时，cosα最小，此时直线PA与抛物线相切，
设直线PA的方程为y=kx+3k-$\frac{\sqrt{6}}{2}$，代入y²=12x，
可得$\frac{k}{12}$y²-y+3k-$\frac{\sqrt{6}}{2}$=0，
∴△=1-4•$\frac{k}{12}$•（3k-$\frac{\sqrt{6}}{2}$）=0，
∴k=$\frac{\sqrt{6}}{2}$或-$\frac{\sqrt{6}}{3}$，
可得切点P（2，±2$\sqrt{6}$），
由题意可得双曲线的焦点为（-3，0），（3，0），
∴双曲线的实轴长为$\sqrt{（2+3）^{2}+（2\sqrt{6}）^{2}}$-$\sqrt{（2-3）^{2}+（2\sqrt{6}）^{2}}$=7-5=2，
∴双曲线的离心率为e=$\frac{2c}{2a}$=$\frac{2×3}{2}$=3．
故选：A．

点评 本题考查抛物线的性质，考查双曲线、抛物线的定义，考查学生分析解决问题的能力，解答此题的关键是明确当m取得最小值时，cosα最小，此时直线PA与抛物线相切，属中档题．