
分析 作差得出$\frac{6{a}^{2}}{9+{a}^{4}}$-1=$\frac{6{a}^{2}-9-{a}^{4}}{9+{a}^{4}}$=-$\frac{({a}^{2}-3)^{2}}{9+{a}^{4}}$分类判断即可得出:点A与点B重合,点A在点B的右侧.的情况.
解答 解:∵$\frac{6{a}^{2}}{9+{a}^{4}}$-1=$\frac{6{a}^{2}-9-{a}^{4}}{9+{a}^{4}}$=-$\frac{({a}^{2}-3)^{2}}{9+{a}^{4}}$
∴①当a=$±\sqrt{3}$时$\frac{6{a}^{2}}{9+{a}^{4}}$-1=0,
∴点A与点B重合,
②当a$≠±\sqrt{3}$时,$\frac{6{a}^{2}}{9+{a}^{4}}$-1>0,
∴点A在点B的右侧.
点评 本题考查了作差法比较大小,难度较小,属于容易题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5或6 | B. | 5或-6 | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
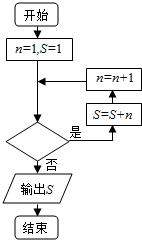 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com