
分析 根据不等式的基本性质可判断①;根据空间线面关系的关系,可判断②;根据等比数列的性质,可判断③;根据对数函数的单调性,可判断④.
解答 解:①若$\frac{1}{a}$<$\frac{1}{b}$<0,则b<a<0,则b2>a2;故正确;
②已知直线l,平面α,β为不重合的两个平面,若l⊥α,且α⊥β,则l∥β或l?β;故错误;
③若-1,a,b,c,-16成等比数列,则b为负值,故b=-$\sqrt{(-1)(-16)}$=-4;故正确;
④设a>b>1,c<0,则logb(a-c)>loga(a-c)>loga(b-c).故正确;
故答案为:①③④.
点评 本题以命题的真假判断与应用为载体,考查了不等式的基本性质,空间线面关系的关系,等比数列的性质,对数函数的单调性,难度中档.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2.+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
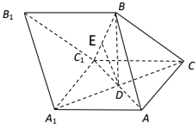 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3+a7≥b2+b6 | B. | a3+a7≤b2+b6 | ||
| C. | a3+a7≠b2+b6 | D. | a3+a7与b2+b6 大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 8 | C. | 4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com