
分析 椭圆的离心率,只需求a、c的值或a、c用同一个量表示.由PF1⊥OX,OP∥AB.易得b=c,a、c的关系.
解答  解:由题意可得PF1=$\frac{{b}^{2}}{a}$,|OF1|=c,|OA|=b,|OB|=a,
解:由题意可得PF1=$\frac{{b}^{2}}{a}$,|OF1|=c,|OA|=b,|OB|=a,
因为PF1⊥OX,OP∥AB,所以$\frac{{|PF}_{1}|}{{|OF}_{1}|}=\frac{\left|OA\right|}{\left|OB\right|}$,即$\frac{{b}^{2}}{ac}=\frac{b}{a}$可得:b=c,
所以a=$\sqrt{2}$c,故e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了椭圆的性质.要充分理解椭圆性质中的长轴、短轴、焦距、准线方程等概念及其关系.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 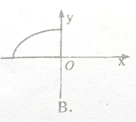 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2π,2016π) | B. | ($\frac{3π}{2},\frac{4031π}{2}$) | C. | (2π,2015π) | D. | (π,2015π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com