
���� ��1������Բ��y����������ཻ�ڵ�M����F1��F2Ϊ��Բ�Ľ��㣬�ҡ�MF1F2�DZ߳�Ϊ2�ĵȱ������Σ������ԲE��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��M��0��$\sqrt{3}$��������$\left\{\begin{array}{l}{y=kx+2\sqrt{3}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���ã�4k2+3��x2+16$\sqrt{3}kx$+36=0���ɴ����ø����б�ʽ��Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ�����ֱ��MA��MB��б��֮��Ϊ��ֵ��
��2�������ҳ���ʽ���㵽ֱ�߾��빫ʽ����������ʽ���������ABM����������ֵ��
��� �⣺��1������ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����y����������ཻ�ڵ�M����F1��F2Ϊ��Բ�Ľ��㣬�ҡ�MF1F2�DZ߳�Ϊ2�ĵȱ������Σ�
��a=2��c=1����b2=4-1=3��
����ԲE��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1����M��0��$\sqrt{3}$����
����$\left\{\begin{array}{l}{y=kx+2\sqrt{3}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���ã�4k2+3��x2+16$\sqrt{3}kx$+36=0��
��=$��16\sqrt{3}k��^{2}-4��36��4{k}^{2}+3��$��0�����k��1.5��k��-1.5��
��A��x1��y1����B��x2��y2������${x}_{1}+{x}_{2}=-\frac{16\sqrt{3}k}{4{k}^{2}+3}$��${x}_{1}{x}_{2}=\frac{36}{4{k}^{2}+3}$��
kMA•kMB=$\frac{{y}_{1}-\sqrt{3}}{{x}_{1}}•\frac{{y}_{2}-\sqrt{3}}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+\sqrt{3}k��{x}_{1}+{x}_{2}��+3}{{x}_{1}{x}_{2}}$
=$\frac{\frac{36{k}^{2}}{4{k}^{2}+3}-\frac{48{k}^{2}}{4{k}^{2}+3}+3}{\frac{36}{4{k}^{2}+3}}$
=$\frac{48{k}^{2}-48{k}^{2}+9}{36}$=$\frac{1}{4}$��
��ֱ��MA��MB��б��֮��Ϊ��ֵ$\frac{1}{4}$��
��2��|AB|=$\sqrt{��1+{k}^{2}��[��-\frac{16\sqrt{3}k}{4{k}^{2}+3}��^{2}-4��\frac{36}{4{k}^{2}+3}]}$=$\frac{4}{4{k}^{2}+3}$$\sqrt{3��1+{k}^{2}����4{k}^{2}-9��}$��
M��0��$\sqrt{3}$����ֱ��l��y=kx+2$\sqrt{3}$�ľ���d=$\frac{\sqrt{3}}{\sqrt{{k}^{2}+1}}$��
���ABM�����S��ABM=$\frac{1}{2}��d��|AB|$=$\frac{1}{2}��\frac{\sqrt{3}}{\sqrt{{k}^{2}+1}}$��$\frac{4}{4{k}^{2}+3}$$\sqrt{3��1+{k}^{2}����4{k}^{2}-9��}$
=$\frac{6\sqrt{4{k}^{2}-9}}{4{k}^{2}+3}$=$\frac{6}{\sqrt{4{k}^{2}-9}+\frac{12}{\sqrt{4{k}^{2}-9}}}$��$\frac{6}{2\sqrt{12}}$=$\frac{\sqrt{3}}{2}$��
���ҽ���$\sqrt{4{k}^{2}-9}$=$\frac{12}{\sqrt{4{k}^{2}-9}}$����k2=$\frac{21}{4}$ʱ����ABM�����ȡ���ֵ$\frac{\sqrt{3}}{2}$��
���� ���⿼����ֱ�ߵ�б��֮���Ƿ�Ϊ��ֵ���ж��������������ε���������ֵ�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ���ҳ���ʽ���㵽ֱ�߾��빫ʽ����������ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��2.5�� | B�� | f��f��2.5���� | C�� | f��f��1.5���� | D�� | f��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
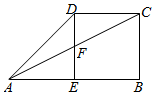 ��ͼ��ABCD��ֱ�����Σ�AB��CD��AB=2CD=2��CD=BC��E��AB���е㣬DE��AB��F��AC��DE�Ľ��㣮
��ͼ��ABCD��ֱ�����Σ�AB��CD��AB=2CD=2��CD=BC��E��AB���е㣬DE��AB��F��AC��DE�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����f��x��=2sin����x+�գ����أ�0��0�ܦաܦУ��IJ���ͼ����ͼ��ʾ������A��B����֮��ľ���Ϊ5����f��x���Ľ���ʽ�ǣ�������
����f��x��=2sin����x+�գ����أ�0��0�ܦաܦУ��IJ���ͼ����ͼ��ʾ������A��B����֮��ľ���Ϊ5����f��x���Ľ���ʽ�ǣ�������| A�� | y=2sin��$\frac{��}{3}$x+$\frac{��}{6}$�� | B�� | y=2sin��$\frac{��}{3}$x+$\frac{5��}{6}$�� | C�� | y=2sin��$\frac{��}{2}$x+$\frac{��}{6}$�� | D�� | y=2sin��$\frac{��}{2}$x+$\frac{5��}{6}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
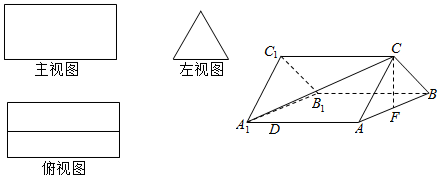
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
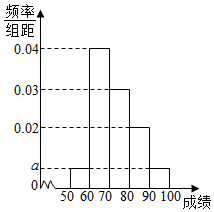 ijУ100��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ��ֲ�������[50��60����[60��70����[70��80����[80��90����[90��100]��
ijУ100��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ��ֲ�������[50��60����[60��70����[70��80����[80��90����[90��100]���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com