
分析 (1)右焦点F2到直线F1B的距离为$\frac{2bc}{\sqrt{{b}^{2}+{c}^{2}}}$=$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,求出a,b,即可求点M的轨迹方程;
(2)分类讨论,直线PQ的斜率存在时,设直线PQ的方程为y=kx+m,代入椭圆方程,消去y,利用OP⊥OQ,可得x1x2+y1y2=0,整理得5m2=4(1+k2),即可得出结论.
解答 解:(1)直线F1B的方程为bx-cy+bc=0,右焦点F2到直线F1B的距离为$\frac{2bc}{\sqrt{{b}^{2}+{c}^{2}}}$=$\sqrt{3}$,
∴2bc=$\sqrt{3}$a,
∵e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴b=1,a=2
∴椭圆M的标准方程$\frac{{x}^{2}}{4}$+y2=1;
(2)点O到直线PQ的距离为定值,设P(x1,y1),Q(x2,y2),
①当直线PQ的斜率不存在时,则△POQ为等腰直角三角形,不妨设直线OP:y=x
将y=x代入$\frac{{x}^{2}}{4}$+y2=1,解得x=±$\frac{2}{5}\sqrt{5}$
所以点O到直线PQ的距离为d=$\frac{2}{5}\sqrt{5}$;
②当直线PQ的斜率存在时,设直线PQ的方程为y=kx+m与$\frac{{x}^{2}}{4}$+y2=1
联立消去y得(1+4k2)x2+8kmx+4m2-4=0.
x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$
因为OP⊥OQ,所以x1x2+y1y2=0,x1x2+(kx1+m)(kx2+m)=0
即(1+k2)x1x2+km(x1+x2)+m2=0
所以(1+k2)$\frac{4{m}^{2}-4}{1+4{k}^{2}}$+km(-$\frac{8km}{1+4{k}^{2}}$)+m2=0,整理得5m2=4(1+k2),
所以点O到直线PQ的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{2}{5}\sqrt{5}$
综上可知点O到直线PQ的距离为定值$\frac{2}{5}\sqrt{5}$.
点评 本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生分析解决问题的能力,弦长公式、韦达定理是解决该类问题的常用知识,要熟练掌握.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
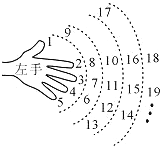 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(2,0,-1) | B. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-1,0,3) | ||
| C. | $\overrightarrow{a}$=(0,-1,-2),$\overrightarrow{b}$=(0,-2,4) | D. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-3,1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
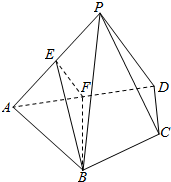 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com